
R언어로 , 스타벅스 매장 데이터를 크롤해서 분석하는 간단한 예제 스크립트입니다.
전체 코드는 글 아래 쪽에 있습니다.
코드 설명
예제에서 하려는 것
간단하게 재미 삼아하는 토이(toy) 분석입니다. 실제 분석 프로젝트에서는 이 보다는 더 심도가 깊게 해야 합니다.
이 분석의 실제 목적은 R로 데이터 크롤을 해서 분석은 어떻게 하는 것인지 설명하는 것입니다. 분석 리포트에서는 크롤한 데이터를 이용해서 인사이트를 도출하고 탐색적데이터분석(EDA)를 어떻게 하는지 예제로 보여줍니다.
이 분석에서 해보려고 하는 것은 스타벅스의 매장 목록을 가져와서 각 시도별, 구군별로 어느 지역에 스타벅스 매장이 가장 많은지 어떤 인사이트가 있는지 살펴보고 또 지역별 인구수와 스타벅스 매장 수와 관계가 있는지를 확인해 보는 간단한 분석입니다.
분석에 들어가기 전에 상식적으로 식음료 판매 매장들은 유동인구가 많은 곳에 자리를 잡는 것이 일반적이기 때문에 당연히 지역별 인구수와 스타벅스 매장 수는 관련이 있을 것이라고 추측할 수 있습니다.
그래서 서울이라면 강남 지역에 스타벅스가 가장 많을 것이라고 추측해 볼 수 있습니다. 서울은 강남에 오피스가 가장 많아서 직장이들도 많고 유동 인구도 많습니다. 정말 그런지 확인은 해봐야 겠지요.
그래서 여기서 확인해 볼 가설은 “스타벅스 매장의 위치는 지역의 인구수 또는 유동인구와 관련이 있을 것이다.” 라는 것입니다.
너무 뻔한 것이어서 굳이 세심하게 분석할 필요가 없다고 생각할지 모르지만 하지만 이미 알고 있거나 너무 뻔한 사실도 실제로 그런지 확인하는 것도 유의미합니다.
의외성이 많아지는 요즘 세상은 알고 있던 상식이 실제와는 다른 경우도 많기 때문입니다.
먼저 알아야 할 것
이 포스트에서 하려는 것을 할 때 꼭 알아야 할 정보와 필요한 것은 3가지입니다.
- 매장의 위치 데이터 제공처
- 매장의 위치데이터 데이터를 크롤(스크랩)하는 법
- 크롤한 데이터를 잘 정제, 정돈하는 법
R언어 사용법 등은 당연히 알아야 하는 것이라 목록에는 안 적었습니다.
Python이나 다른 언어로 해도 되지만 여기서는 R언어로 하겠습니다.
데이터를 얻어 오는 곳
이런 정보가 어디 있는지는 검색을 해서 알아내야 합니다. 검색해보니 대충 아래와 같은 것이 제일 만만해 보입니다.
- 스타벅스: https://www.starbucks.co.kr
- 시군구별 인구데이터: https://kosis.kr
먼저 스타벅스 매장 주소 데이터는 스타벅스 웹사이트에서 가져오면 되는데 csv나 엑셀 파일로 다운로드하게 지원하지 않으니 웹페이지의 내용물을 읽어서 파싱(parsing)해야 합니다.
이 작업은 웹 스크랩이라고 하는데 흔히 크롤이라고 부릅니다. 사실 원래 크롤과 스크랩은 서로 차이가 많습니다만 이 글에서는 그냥 널리 알려진 대로 크롤이라고 하겠습니다.
또 스타벅스 웹페이지는 지도상에 매장의 위치를 표시하기 위해서 Ajax로 데이터를 호출하는 방식을 사용하는데 이것의 방식을 알아내서 어떻게 데이터를 가져와야 하는지도 알고 있어야 합니다.
보통 크롬이나 파이어폭스의 개발자도구를 사용해서 알아내는데 연습과 방법을 익히는데 시간과 노력이 필요합니다. IT활용능력, 웹개발능력과 관련이 있는 것이라서 이것까지 설명하려면 설명이 길어지므로 이것을 알아내는 방법은 여기서는 생략합니다. 다음 기회에 다른 포스트에서 하겠습니다.
이 글에 소스코드를 넣어 두었으니 이미 완성된 코드를 참고 참고하세요.
인구데이터는 국가통계포털 웹사이트에서 가져오면 됩니다. csv나 excel로 다운로드 할 수 있게 지원하므로 매우 편합니다만 그래도 역시 데이터 정제, 정돈 작업은 좀 필요합니다.
인구데이터는 여기 말고도 받을 수 있는 곳이 더 있습니다. 더 편한곳이 있으면 그냥 거기를 이용하세요.
데이터를 크롤하는 법
R언어는 텍스트 파일을 파싱하거나 json 데이터를 처리하는 것이 조금 복잡한 편에 속합니다. R언어가 수치와 벡터 계산에 중점을 두기 때문에 이런 텍스트 처리에는 매우 약합니다.
하기가 까다롭다는 말입니다.
이런 것을 하려면 Python이나 Javascript가 더 나은 선택이지만
R언어로 이걸 하면 한 코드에서 데이터 크롤, 정제, 분석, 시각화까지 한 번에 할 수 있어 관리가 편하고 나중에 코드를 다시 볼 때 전체 흐름을 이해하기 편하다는 장점이 있습니다.
어쨌든 R언어에서 httr, urltools, jsonlite 패키지의 사용법을 익히면 됩니다.
데이터 정제, 정돈
데이터랭글링이라는 것을 할 텐데 이런 작업은 tidyverse 패키지에 포함된 여러 패키지를 이용하는 것이 가장 세련되고 좋은 방법입니다.
그리고 시각화는 ggplot2를 사용하겠습니다.
결과
스타벅스 전체 매장수: 1658개
1658개로 나옵니다. 스타벅스는 모두 신세계에서 운영하는 직영점이라고 알려져 있고 관리가 웹사이트 관리가 잘 되고 있을 것이라고 생각돼서 이 수치는 맞을 것입니다.
수천개는 될 것 같지만 제 예상보다는 적습니다.
시도별 매장수
sido n
<chr> <int>
1 서울특별시 571
2 경기도 383
3 부산광역시 128
4 대구광역시 71
5 인천광역시 67
6 경상남도 66
7 광주광역시 59
8 대전광역시 59
9 경상북도 48
10 충청남도 36
11 울산광역시 29
12 전라북도 29
13 강원도 28
14 충청북도 26
15 전라남도 25
16 제주특별자치도 22
17 세종특별자치시 11시도별 매장수는 역시 서울이 가장 많고 그 다음은 경기도, 부산 순입니다. 인구수가 많은 시도에 매장이 더 많은 것을 알 수 있습니다.
네 당연하죠. 물론 지역별로 로컬 카페나 다른 프렌차이즈, 브랜드의 커피매장이 더 인기가 있는 지역이 있을 수도 있으니 이 가설이 틀렸을 여지는 있습니다.
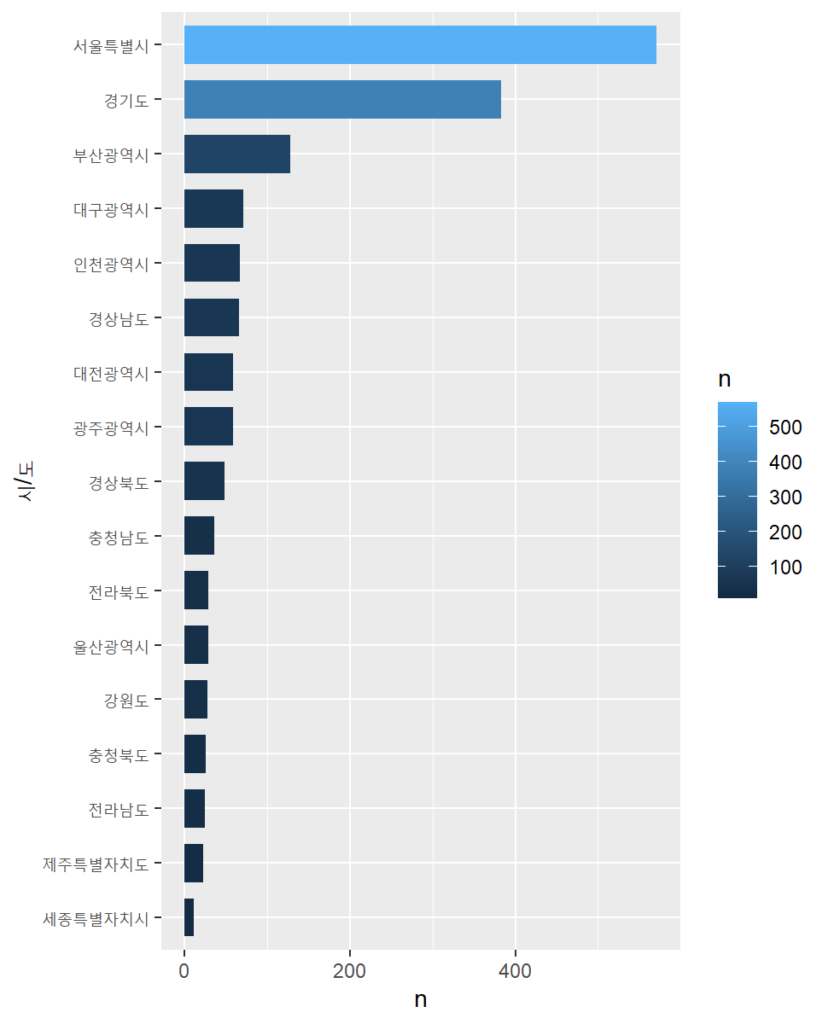
차트로 보며 시도별 매장수의 규모를 더 직관적으로 확인할 수 있는데 서울특별시와 경기도를 합치면 다른 시도를 다 합친 것 보다 더 많습니다.
우리나라 스타벅스 매장은 수도권에 크게 집중되어 있습니다.
구군별 매장수
sido gugun n sido_gugun
<chr> <chr> <int> <chr>
1 서울특별시 강남구 88 서울특별시 강남구
2 서울특별시 중구 52 서울특별시 중구
3 서울특별시 서초구 48 서울특별시 서초구
4 경기도 성남시 47 경기도 성남시
5 경기도 고양시 42 경기도 고양시
6 서울특별시 영등포구 40 서울특별시 영등포구
7 서울특별시 종로구 39 서울특별시 종로구
8 경기도 수원시 35 경기도 수원시
9 경기도 용인시 34 경기도 용인시
10 서울특별시 송파구 34 서울특별시 송파구 구군별로 매장수를 살펴보면 역시 서울 강남구가 가장 많습니다. 한국에서 아마 인구밀도가 가장 높은 지역이며 유동인구와 일과시간에 직장인이 가장 많이 있는 곳입니다.
그 다음은 역시 유동인구가 가장 많고 오피스밀집 지역이며 인구밀도가 높은 서울 중구입니다. 중구에는 명동, 충무로, 을지로가 있습니다.
그 다음은 서울 서초구인데 서초구는 강남구와 인구밀도는 비슷하지만 오피스공간 보다는 주거지역이 훨씬 많기 때문에 강남구나 중구에 비해서 낮시간에 직장인이 아주 많지는 않습니다. 그래도 괘나 많습니다.
그리고 그 다음은 경기도 성남시인데 성남에는 분당과 판교가 있으며 성남전체의 인구도 많으므로 이것도 당연합니다.
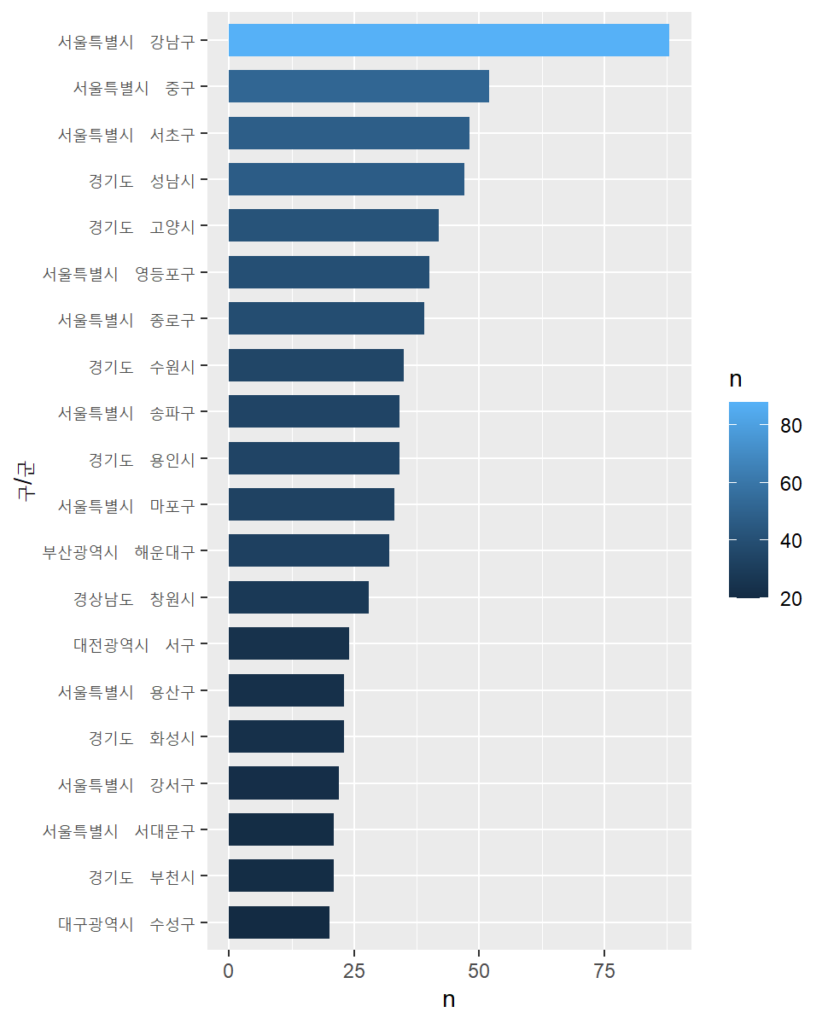
서울-강남구에 스타벅스가 압도적으로 많으며 다른 대형 지역구들도 제법 많습니다. 앞서 말했듯이 이 지역은 직장인들이 주중에 많이 머무는 지역들입니다. 물론 여기 나온 인구수는 거주 인구수이기 때문에 직장인이 주중에 많다는 것과의 상관관계를 다시 확인해야 할 필요가 있습니다만 알려진 바로는 매우 특별한 경우를 빼면 거주인구가 많은 지역에 직장도 많습니다.
인구수와 매장수의 상관관계
Pearson's product-moment correlation
data: sido_tbl$n and sido_tbl$total
t = 7.6707, df = 15, p-value = 1.439e-06
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7216524 0.9609928
sample estimates:
cor
0.8926678 시도별 인구수와 스타벅스 매장수의 상관관계를 보면 상관계수가 0.89로 강한 상관이며 검정에서 대립가설 채택으로 상관이 있다는 결과가 나옵니다.
더 해볼 것
상관관계를 볼 때 단순 인구수가 아닌 면적을 인구수로 나눠서 인구밀집도를 구한 다음에 상관관계를 보는 것이 더 합리적이겠지만 면적데이터를 가져와서 붙여야 하니 귀찮아서 생략하겠습니다.
또 구군별로도 면적데이터를 가져와서 구군별로도 인구수와 스타벅스 매장수가 상관이 있는지 확인해 보는 것도 필요합니다만 이것도 생략하겠습니다.
혹시 해보고 싶으시면 아래 소스를 보시고 고쳐서 직접 한 번 해보세요.
결론 및 인사이트
매장수와 지역의 인구밀집도는 관계가 있습니다.
시도별, 구군별로 모두 상관관계가 있습니다.
따라서 스타벅스매장이 많은 곳은 인구밀집도가 높은 지역일 가능성이 큽니다.
인구밀집도는 유동인구수와 상관관계가 있는 것으로 알려져 있습니다.
스타벅스 매장이 많은 곳(있는 곳)은 유동인구가 많은 곳입니다.
마약 누군가 많은 유동인구가 필요한 점포를 개업하려고 한다면 스타벅스 부근에 개점하면 됩니다.
길거리 음식을 팔거나 판매하려면 패션 팟업스토어, 푸드 트럭을 열려면 스타벅스 근처에 하면 잘 될 것입니다. 물론 그게 가능하다면 말이죠.
전체 스크립트
소스 파일
https://github.com/euriion/r-exams/blob/main/starbucks_analysis.R
소스 내용
# 스타벅스 목록을 읽어서 간단한 통곗값을 출력하는 R 스크립트
# install.packages(c("httr", "urltools", "jsonlite"))
library(httr)
library(urltools)
library(jsonlite)
# 데이터를 긁어올 사이트: https://www.starbucks.co.kr
# 시도 목록을 가져오는 부분
url <- "https://www.starbucks.co.kr/store/getSidoList.do"
res_content <- POST(url)
res_object <- fromJSON(content(res_content, "text"))
sido_items <- tibble(sido_nm=res_object$list$sido_nm, sido_cd=res_object$list$sido_cd)
# 구군 목록을 가져오는 코드. 구군은 분석에 필요하지 않으므로 리마킹
# url = "https://www.starbucks.co.kr/store/getGugunList.do"
# post_params = "sido_cd=01&rndCod=4X93H0I94L"
# res_content <- POST(url, body=parse_url(sprintf("%s?%s", url, post_params))$query)
# res_object <- fromJSON(content(res_content, "text"))
# 각 시도별 주소를 가져오는 부분
url <- "https://www.starbucks.co.kr/store/getStore.do"
payload <- "in_biz_cds=0&in_scodes=0&search_text=&p_sido_cd=08&p_gugun_cd=&in_distance=0&in_biz_cd=&isError=true&searchType=C&set_date=&all_store=0&whcroad_yn=0&P90=0&new_bool=0&iend=1000"
post_params <- parse_url(sprintf("%s?%s", url, payload))$query
res_content <- POST(url, body = post_params)
res_object <- fromJSON(content(res_content, "text"))
# 시도 코드와 이르을 받아서 주소목록이 들어 있는 data.frame을 리턴하는 함수
get_addrs <- function(sido_cd, sido_nm) {
url <- "https://www.starbucks.co.kr/store/getStore.do"
payload <- sprintf("in_biz_cds=0&in_scodes=0&search_text=&p_sido_cd=%s&p_gugun_cd=&in_distance=0&in_biz_cd=&isError=true&searchType=C&set_date=&all_store=0&whcroad_yn=0&P90=0&new_bool=0&iend=10000", sido_cd)
post_params <- parse_url(sprintf("%s?%s", url, payload))$query
res_content <- POST(url, body = post_params)
res_object <- fromJSON(content(res_content, "text"))
cbind(rep(sido_cd, length(res_object$list$addr)), rep(sido_nm, length(res_object$list$addr)), res_object$list$addr)
}
# 데이터랭글링
# install.packags(c("tidyverse", "stringi"))
library(tibble)
library(dplyr, warn.conflicts = FALSE)
library(stringi)
df <- sido_items |> rowwise() |> mutate(addr=list(get_addrs(sido_cd, sido_nm)))
tbl <- do.call(rbind.data.frame, df$addr)
names(tbl) <- c("sido_cd", "sido_nm", "addr")
tbl <- tbl |> rowwise() |> mutate(addrsplit=stri_split_fixed(addr, " ", 4))
tbl <- as_tibble(do.call(rbind.data.frame, tbl$addrsplit))
names(tbl) <- c( "sido", "gugun", "dong", "bunji")
tbl |> count() # 전체 매장 개수
stat_sido <- tbl |> count(sido) |> arrange(desc(n)) # 시도별 매장 수
stat_gugun <- tbl |> count(sido, gugun) |> arrange(desc(n)) |> mutate(sido_gugun=paste(sido, " ", gugun)) # 시도별 매장 수
# 시각화
library(ggplot2)
p <- ggplot(stat_sido, aes(x =reorder(sido, n), y = n)) +
geom_col(aes(fill = n), width = 0.7)
p <- p + coord_flip()
p <- p + xlab('시/도')
p
p <- ggplot(head(stat_gugun, 20), aes(x =reorder(sido_gugun, n), y = n)) +
geom_col(aes(fill = n), width = 0.7)
p <- p + coord_flip()
p <- p + xlab('구/군')
p
# 데이터 출처: # https://kosis.kr/statHtml/statHtml.do?orgId=101&tblId=DT_1B040A3&checkFlag=N
pop_sido_text_data <- "sido,total,male,female
서울특별시,9505926,4615631,4890295
부산광역시,3348874,1638207,1710667
대구광역시,2383858,1174667,1209191
인천광역시,2949150,1476663,1472487
광주광역시,1441636,713037,728599
대전광역시,1451272,724026,727246
울산광역시,1121100,575939,545161
세종특별자치시,374377,186907,187470
경기도,13571450,6830317,6741133
강원도,1538660,774315,764345
충청북도,1597097,810548,786549
충청남도,2118638,1083242,1035396
전라북도,1785392,888291,897101
전라남도,1832604,922190,910414
경상북도,2624310,1322509,1301801
경상남도,3311438,1666968,1644470
제주특별자치도,676691,339071,337620
"
pop_sido_tbl <- read.csv(textConnection(pop_sido_text_data))
sido_tbl <- pop_sido_tbl |> inner_join(stat_sido, by = "sido")
# 상관계수
cor(sido_tbl$n, sido_tbl$total)
# 결괏값: 0.8926678
cor.test(sido_tbl$n, sido_tbl$total)
여기까지 입니다.