지금 하는 일과 관련이 있는 것이라서 zdnet기사에 앱넥스트라는 회사에서 제안했다고 하는 타임라인 타겟팅이라는 기법(아이디어)에 대한 기사를 스크랩해 놓은적이 있는데 내용도 정리할겸 그림툴도 써볼겸(사실은 이게 본래의 포스팅 목적입니다 ‘ㅡ’;;) 해서 포스트를 올립니다.
직접 기사를 읽어보시면 되겠지만 저는 그림툴을 사용해 보는 것이 목적이므로 정리를 좀 해보자면 이렇습니다.
최근의 앱인스톨 광고 그러니까 앱인스톨을 유도하는 배너 광고들이 실적이 좋지 않다고 합니다. 그 이유 중의 하나가 이제 사람들은 자기 스마트폰에 더 이상 새로운 앱을 설치하지 않는다고 합니다.
- 이미 필요한 것을 대부분 설치했고 사용하는 것들이 몇개에 한정되어 있기 때문입니다.
- 그리고 필요한 것이 생기면 그때그때 찾아서 설치해도 되니 미리 설치해 둘 필요는 없습니다.
- 게임이 아니라면 그런 배너에 반응을 잘 안하게 되는 게임도 설치 광고가 그렇게 큰 효과를 보지 못한다는 말이 많습니다. (다 그런것은 아니겠지만요)
그래서 위 기사에서 말하는 아이디어는 이렇습니다.
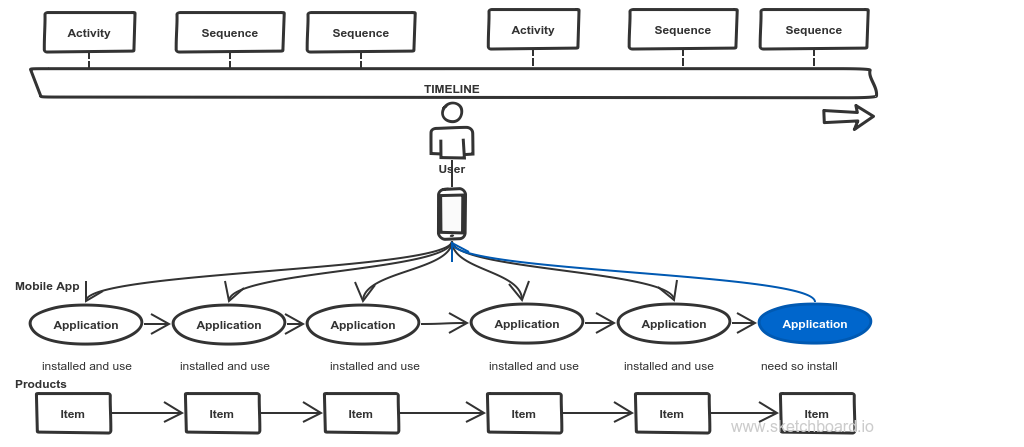
일종의 개인화 타겟팅(personalized targeting)인데 위의 그림처럼 사람들의 타임라인을 추적(감시한다기 보다는 엿본다는 것이 맞겠습니다)해서 상황들을 모니터링하다가 특정 상황이 되면 그 상황에 필요한 앱인데 아직 사용자가 설치하지 않은 앱이 있다면 광고로 추천해서 바로 설치하도록 유도한다는 것입니다.
그러기 위해서 사용자가 사용하고 있는 스마트폰에 항상 사용자의 액션을 모니터링하는 앱이 필요한데 사실 대부분의 회사들이 이걸 하기가 현실적으로 불가능합니다. 스마트폰의 모든 상황을 전역으로 감시하는 장치를 스마트폰에 심을 수가 없기 때문입니다.
앱넥스트라는 회사는 자사의 SDK(스마트폰 애플리케이션에 광고를 노출할 수 있도록 해주는 킷)를 사용한 제휴 앱들을 이용해서 사용자의 행적(activity)를 보고 있다가 다른 앱을 설치하도록 유도할 수 있다는 것입니다. 알려주는 것은 아마 Push 기능 같은 것을 사용하지 않을까 싶습니다.
실현이 가능하다면 “앱을 설치할 수 밖에 없는 적절한 상황을 찾아서 그때 광고를 보여주면 설치를 많이 하겠지” 라는 것을 이용한 것인데요.
이걸 하기 위해서는 사실 앱 매체(광고를 보여주는 앱들)을 많이 제휴하고 있어서 그 앱들을 사용자가 늘 쓰고 있거나 빈번하게 쓰고 있어야 합니다. 즉 앱 매체 커버리지가 좋아야 합니다. 이것은 사실 진입장벽이 매우 높아서 말이 후발주자(모바일 광고 플랫폼 회사)들이 제휴한 앱들이 많지 않으면 힘듭니다. 아니면 끝판왕 하나를 제휴하던지요(카카오톡 같은 것?)
위의 앱 매체 제약 조건이 걸린다면 일반적인 PC 온라인 광고에서는 응용할 수 있는 방법은 라이프타임에 대한 모니터링을 길게 해서 상품을 추천해 주는 방법을 얼른 생각해도 할 수 있을것만 같습니다.
어떤 온라인 사용자가 추정 모델 또는 데이터온보딩(data on-boarding)으로 20대 여성이라는 것을 알고 다음과 같은 순서로 제품에 관심을 보였거나 구매를 했다면 그 다음 상황에 필요한 것을 유추해서 추천해 줄 수 있습니다.
청바지 → 워킹용 신발 → 워터프루프 화장품 → 수영복 → 카메라방수팩
다소 억지로 만든 예입니다만 저런 시퀀스가 있다면 카메라방수팩을 광고해서 구매하도록 유도할 수 있습니다. 물론 이것도 앱매체의 커버리지 문제처럼 온라인 웹페이지와 제휴가 많이 되어 있어야 하고 제품도 골고루 보여줘서 어떤 행동(behavior)를 하는지 시차를 두고 기록해 둬야 하는 문제가 있습니다. 물론 광고에 잘 반응하는 사람일 수록 하기 쉽고 그렇지 않은 사람이나 특정 쇼핑몰(G마켓 이랄지)에서만 구매를 하는 사람들이라면 조금 어렵습니다.
이런 사람들에게는 다 포기하고 조건을 만족하는 사람들에게만 해도 충분할 것 같은 느낌입니다.
필요한 상품의 세트나 연관상품의 세트는 데이터만 있다면 노출이나 클릭, 구매 기록으로부터 연관 규칙 탐사(sequence association rule mining)같은 간단한 방법으로도 정보를 추출해서 확보 할 수도 있을 것 같은데 실제로 해보지는 않았지만 간단한 시뮬레이션 정도는 해볼 수 있을 것 같습니다.
다시 앱의 문제로 돌아와서 만약 카카오톡 같은 사람들이 매우 많이 쓰는 앱이라면 사용자의 메세지 텍스트를 분석해서 (윤리적으로 그러면 안되는 것은 당연하고) 문맥을 파악한 뒤 필요한 것을 알아내서 카톡내에서 광고를 보여주고 추천해 주는 방법도 고민해 볼 수 있겠습니다. (그냥 상상입니다. 현실적으로 안되겠지요)


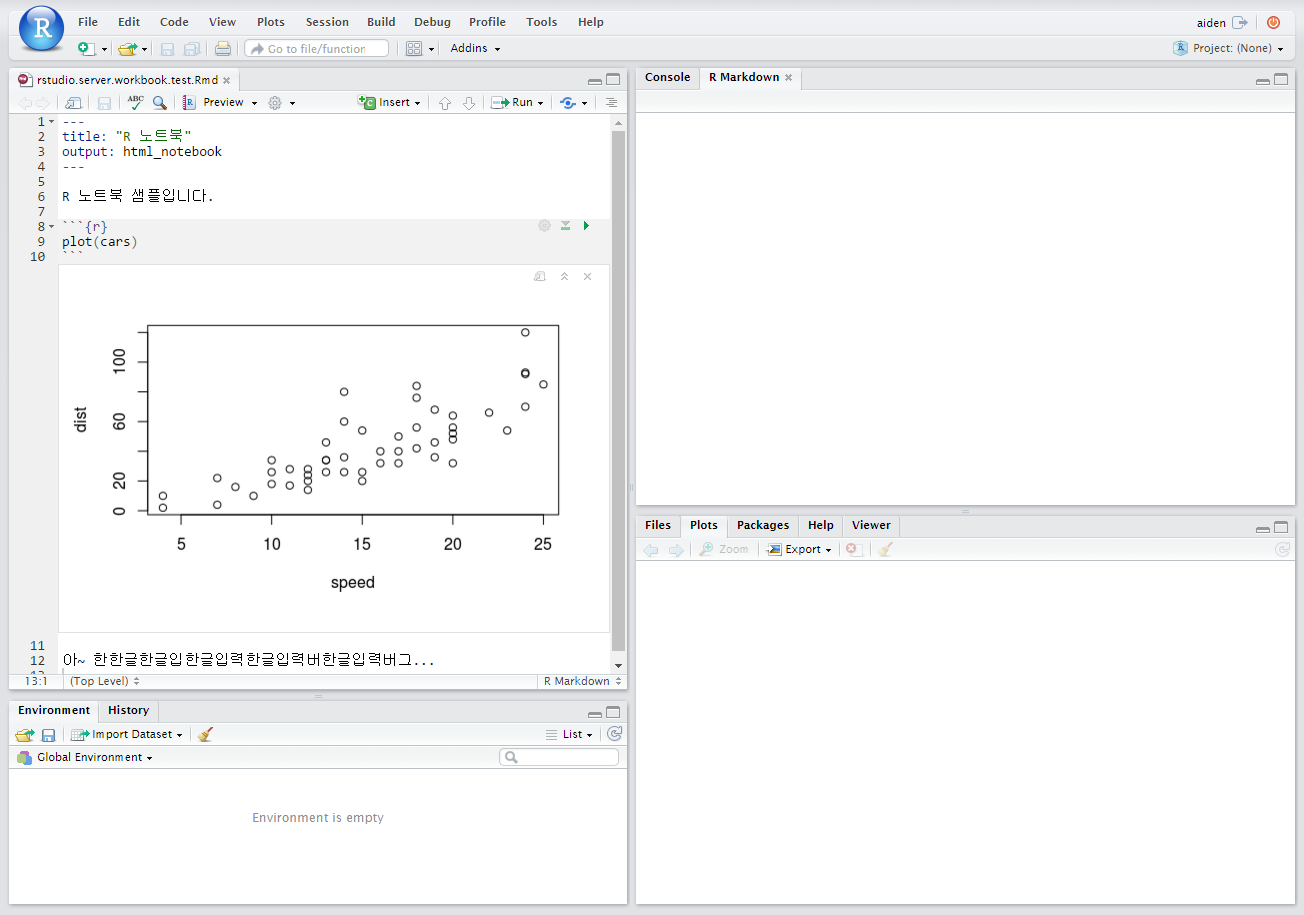 기능은 RStduio desktop 처럼 깔끔하게 잘 작동합니다.
기능은 RStduio desktop 처럼 깔끔하게 잘 작동합니다.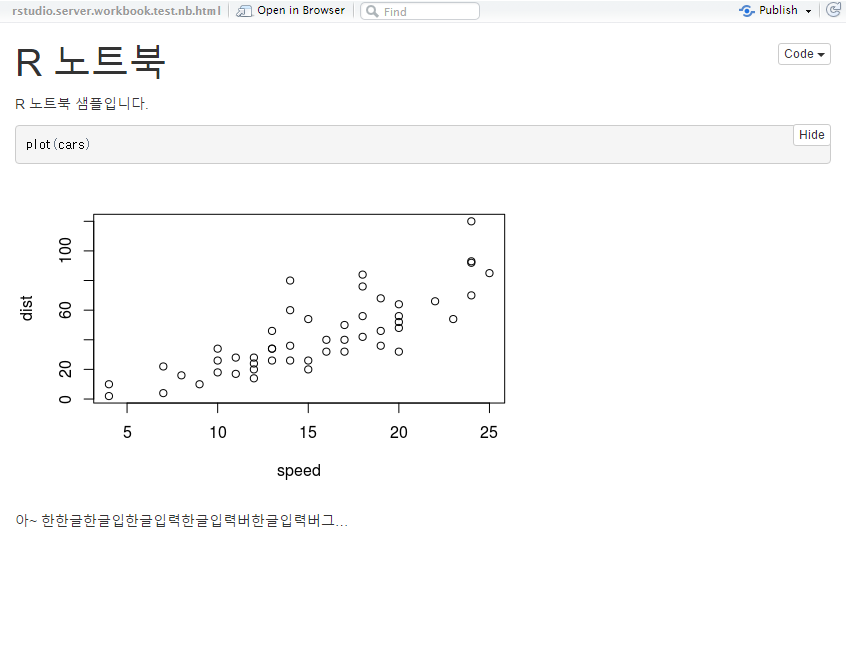 미리보기(preview) 기능도 잘 작동을 합니다.
미리보기(preview) 기능도 잘 작동을 합니다.