구글, 빙, 네이버, 다음과 같은 검색포털에 접속해 보면 상단에 검색창이 있습니다.
이 검색창에 정보를 찾기 위해서 검색어를 입력하는데 이때 키보드를 타이핑할 때마다 검색창 바로 아래에 지금까지 타이핑한 글자들로 구성된 검색어 목록을 보여주고 선택을하면 검색어를 다 입력해주는 검색어 자동완성 기능이 있습니다.
검색어를 타이핑하다 말고 마우스나 키보드로 완성된 검색어를 입력할 수 있게 해주기 때문에 “검색어 자동완성”이라고 합니다.
데이터사이언스와 크게 관련이 없긴 하지만 검색어 자동완성에 대한 내용을 적어보겠습니다.
사실 추천되는 검색어 목록을 만드는 것이 데이터사이언스와 관련이 많이 있습니다만 내용이 너무 길어지니 이것은 나중에 설명하겠습니다.
앞서 설명했지만 “검색어 자동완성”은사용자가 검색어를 힘들게 다 입력하지 않아도 입력 도중의 단어로 시작하거나 또는 포함하는 단어들을 목록으로 보여주고 선택해서 검색어를 바로 완성하게 해주는 사용자 친화적 (user friendly) 기능(서비스)입니다.
아래의 그림처럼 구글에서 검색어를 입력하면서 볼 수 있는 이런 것입니다.
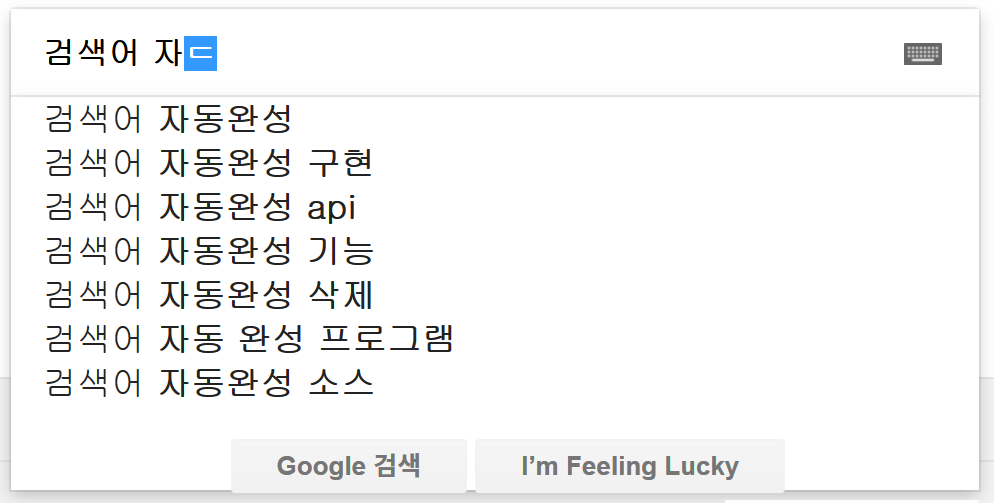
네이버, 다음, 빙, 야후, 덕덕고(duckduckgo)와 같은 검색포털과 각종 온라인 쇼핑몰, 오픈 마켓, 온라인 서점에서도 모두 볼 수 있습니다.
검색어 자동완성은 서비스와 사용자의 행동 유도 관점에서 각각 장단점이 있습니다. (행동과학의 관점입니다)
장점
- 사용자 편의성
- 검색서비스를 이용하는 사람들이 타이핑이 불편하거나 느린 경우 편하게 원하는 검색어를 입력할 수 있게 해줍니다.
- 사용자가 오타를 입력해서 검색결과를 찾지 못하는 것을 방지해줍니다
- 검색어가 잘 생각나지 않을때 단어의 파편을 입력해서 목록을 보고 기억나지 않은 또는 부분적으로만 기억나는 단어를 입력해서 검색어를 입력할 수 있습니다.
- 다른 사용자가 많이 입력하는 검색어가 제안되기 때문에 사람들이 많이 입력하는 최신 트렌드의 검색어를 자신도 입력해서 최신 자료를 입수 할 수 있습니다.
- 포털의 이득
- 사용자가 찾을 것이 없어도 뭐라도 제안을 해서 검색을 하게 만듭니다. 즉 사용자 입력할 검색어를 마땅히 기억하지 못해 검색 포털을 떠나는 것을 방지할 수 있습니다.
- 상업적으로 유리한 검색어를 자동완성에 넣어서 상업적 이득을 볼 수 있습니다.
단점
- 사용자의 새로운 경험 박탈
- 사용자의 입장에서는 검색어를 잘못 입력해서 뜻하지 않게 좋은 자료나 괜찮은 자료를 찾을 수 있는 예외적인 경험을 할 수 있는 기회가 줄어듭니다. 사용자가 실수할 것을 방지해주니 장점이라고 볼 수도 있긴합니다.
- 검색어는 인기 검색어나 사람들이 자주 입력하는 단어를 기반으로 추천되기 때문에 다른 사람들도 많이 검색하는 단어를 사용하기 때문에 정보 입수의 다양성에 반하게 됩니다. 일종의 개성없는 정보의 편식을 만듭니다. 반면 장점이기도 하겠습니다.
사용자의 입장에서는 어쨌든 단점보다는 장점이 더 많은 것 같습니다. 편하니까요. 하지만 가끔 검색어 자동완성이나 인기검색어로 정보의 섭취를 유도당하고 있는 것은 아닌지 생각해 봐야 합니다.
자동완성에 나오는 목록에 광고 목적으로 목록에서 위에 위치하도록 되어 있는 것도 있다는 것을 아셔야 합니다.
이제 구현 또는 구축에 대한 것을 적어보겠습니다. 기술적으로 보면 자동완성 시스템을 만들어서 운영하는 것은 생각보다 녹녹하지 않습니다. 자동완성은 포털 뿐만 아니라 소셜네트워크 서비스에서도 볼 수 있고 쇼핑몰, 인터넷서점, 그리고 사내 인트라넷 같은 곳에서도 볼 수 있습니다. 하지만 구현되어 있는 것도 다르고 각각의 상황에 따라 운영 방식이나 상태도 다를 것입니다.
구현이나 운연에 관련된 부분을 Frontend, Backend, Data processing 3단계로 나눠서 설명해 보겠습니다.
Frontend 부분
Frontend 부분은 당연히 Javascript로 합니다. Ajax입니다. 사용자가 키보드를 타이핑할 때마다 backend로 사용자가 입력 중인 단어를 보내서 제안할 검색어 목록을 받아서 화면에 뿌려줍니다.
주의할 점은 사용자의 타이핑이 매우 빨라서 제안된 검색어가 화면에 보여지기 전에 사용자가 빠르게 타이핑을 하면 기존에 타이핑했던 요청(backend call)이나 지금 막 하고 있었던 자동화면창 표현(rendering)을 중단하고 다시 backend 호출을 하는 트릭이 필요합니다. 그렇게 하지 않으면 사용자에게 불편한 경험을 주게 됩니다. (눈으로 볼 때 거리적 거려서 불안감을 줍니다)
예를들어 “자동완성”이라는 검색어를 사용자가 포털의 검색창에 입력한다면 사용자는 다음과 같은 순서로 빠르게 키보드를 쳐나가게 됩니다.
- ㅈ
- 자
- 잗
- 자도
- 자동
- …
타이핑이 빠른 사람이라면 1 ~ 2초이내에 12번의 타이핑을 하게 됩니다. 12번의 backend 호출이 일어나게 되는데 사용자가 타이핑을 멈추거나 잠시 쉴때까지는 불필요한 호출이기 때문에 생략하는 기술이 필요합니다.
물론 요즘은 javascript 라이브러리들이 잘 구현된것이 많아서 잘 된 것을 찾아서 갖다 쓰면 됩니다.
jquery autocomplete: https://jqueryui.com/autocomplete/
하지만 좀더 빠르고 잘 작동하는 것을 만드려면 직접 만드는 것이 좋습니다.
Backend 부분
backend 부분은 다양한 방법으로 구현이 가능하고 사이트의 규모나 동시 접속하는 사용자의 수같은 상황에 따라 쓸 수 있는 방법이 달라집니다. 여러 방법을 선택할 수 있습니다.
Javascript 색인 방식
몇개의 library가 잘 공개된 것이 있습니다. 이 방식은 Javascript로 자동완성에 사용할 검색어를 모두 N-gram 색인 구조로 만들어서 웹브라우저에 로딩한 후 사용하는 방식입니다.
데이터의 사이즈가 커지면 성능저하가 심하고 검색어 데이터가 대량(수천만 또는 수억)이 되면 아예 불가능 합니다.
웹페이지를 로딩할 때 데이터를 한꺼번에 로딩해야 하기 때문에 웹페이지 렌더링을 방해하거나 또는 렌더링이 된 후에도 초기에 잠깐 작동하지 않는 불편함이 생깁니다.
데이터가 적을 때 씁니다. python 문서화 패키지인 sphinx 같은 것이 static html에서 문서검색을 할 수 있게 하기 위해서 이런 것을 사용하는 것을 볼 수 있습니다. 일부 위키시스템도 이 방식을 사용합니다.
이 경우는 사실 backend가 하는 일이 별로 없긴합니다.
데이터베이스의 like query를 이용하는 방법
데이터베이스에 대놓고 like 구문을 보내서 검색하는 무식한 방식입니다. 무식하지만 쉽고 구현하기 쉽습니다. 데이터가 적고 접속 사용자도 적을 때 막 사용할 수 있는 방법입니다.
SELECT name
FROM products
WHERE name like '%자동%'
물론 DB의 full-text 검색 기능을 이용하거나 memory table 기능을 이용하거나 아니면 in-memory 데이터베이스등을 이용해서 성능을 개선할 수 있겠지만 대용량 트래픽을 받아야 하는 상황이면 DB가 이런 과부하를 견디기 어렵습니다.
유사한 방법으로 Sphinxsearch 같은 것을 쓰고 cache 를 덧대주는 방법도 있겠습니다. 그런데 Sphinxsearch는 검색엔진입니다.
Static file을 이용하는 방법
모든 예상되는 입력에 대해서 json file같은 것을 static 모두 생성(generation) 한 후에 static content server에 올려놓고 frontend에서 요청이 오면 이 파일을 그대로 당겨서 전달하는 방식입니다. 과거 어떤 포털이 이 방식을 사용했다고 합니다. 너무 무식하긴 하지만 성능은 괜찮은 방법입니다.
이것도 backend에서 하는 것은 요청한 입력에 대한 맞는 파일을 찾아서 읽은 후에 입력한 키워드에 맞는 목록 데이터를 던져주면 됩니다.
NoSQL을 이용하는 방법
memcache를 쓰거나 NoSQL 중에 반응속도가 빠른 것을 마련하고 static file 생성하는 방식처럼 모든 입력에 해당하는 키워드와 그 키워드들의 조합파편을 key로 하고 value에 검색어 제안목록을 넣어두고 요청이 올 때마다 빼서 던져주는 방식입니다.
저는 안해봐서 잘 모르겠습니다만 성능은 괜찮다고 하는 것 같습니다. 솔직히 이렇게는 안하고 싶습니다. 메모리 효율이 좀 안좋을 것 같습니다.
트리 구조(tree structure)를 이용한 대몬(Daemon)을 사용하는 방법
가장 많이 쓰이는 방법입니다. 성능도 좋고 추가 기능을 넣을 수가 있기 때문입니다. 과거에는 이런 대몬(daemon)을 직접 개발해야 하는 것이 상당히 어렵고 고통이었지만 지금은 좋은 오픈소스가 있습니다.
이 방식은 트리 자료구조(알고리즘) 중에 적합한 것을 선택해서 빠르게 HTTP 리턴을 할 수 있는 경량 웹서버를 만드는 것입니다. Frontend에서 요청이 오면 트리탐색을 해서 트리의 하위 노드들을 모두 취합(또는 적당히 정해진 갯수만 취합해서)해서 자동완성 제안 목록을 만들고 트리 노드에 붙어 있는 value(score같은 것입니다)를 보고 역순 정렬을 하거나 해서 검색어 추천 목록 정해진 갯수만큼 뽑아서 리턴합니다. 보통 리턴해줘야 하는 자동완성 검색어 목록은 20 ~ 30개이면 됩니다.
트리 자료 구조는 보통 Trie나 FSA(Finite State Automata)를 사용하거나 유사한 것을 사용합니다. 요즘은 더 괜찮은 것들이 있을지도 모르겠습니다.
구현할 때 몇가지를 고려해야 합니다.
- 자체 캐시(Cache)
- 자체 캐시를 지원해야 합니다. 자동완성을 위해서 backend의 앞쪽에 캐시를 붙여서 성능강화를 할 수도 있습니다만 자료구조내에서 데이터를 탐색하는 것도 로드가 발생하기 때문에 LRU같은 간단한 캐시 기능을 넣어야 합니다.
- 랭킹(ranking)
- 제안할 목록의 랭킹도 고려해야 합니다. 보통 검색어 제안 목록을 가나다 순이 아니라 스코어를 주고 그 순서로 보여주는 것이 사용자 경험상 더 낫기때문입니다.
- 그래서 빠른 소팅(sorting) 라이브러리를 사용하거나 만들어야 합니다.
- 메모리 페이징 문제
- 추천하는 검색어 목록을 모두 메모리에 가지고 있을 수 있다면 그렇게 해야 합니다. 목록을 저장하기 위해서 디스크를 사용하면 페이징(paging)을 할 때 성능저하가 크기 때문에 가능한 메모리를 최대한 활용해야하고 디스크를 쓰더라도 SSD를 써야합니다.
- 클러스터링
- 디스크를 사용하지 않고 메모리에서만 처리하겠다고 하면 데이터가 많아질때 여러 서버에 분산하는 것이 필요합니다. 그런데 트리구조는 분산하기 굉장히 어렵습니다.
- 온라인 업데이트
- 데이터를 주기적으로 갱신해 주어야 하는데 가동중인 대몬을 멈추고 업데이트하기 보다는 대몬을 가동시킨 상태에서 데이터를 업데이트를 해야합니다.
- 물론 로드밸런서(load balnacer) 같은 것을 두고 로드밸런서 뒤에 붙어 있는 서버의 대몬을 순차적으로 재시작해가면서 데이터를 갱신하는 방식을 사용할 수도 있습니다. 피곤하지요.
위의 것들은 구현할 때 고려할 내용이긴 하지만 오픈소스를 선택할 때 어떤 기능을 지원하는지 확인하는데 필요할 것 같습니다. 오픈소스 검색어 자동완성 대몬은 몇개 없습니다. 가장 잘 알려진 것은 아래 2개입니다.
- Linked-in Cleo
- Duck-duck-go libface
Cleo(클레오)는 라이브러리인데 Cleo를 바로 쓰기 보다는 Cleo-Primer라는 Cleo를 이용한 응용구현체의 소스를 받아서 빌드하고 설명서대로 데이터를 XML로 http 로 부어넣으면 온라인 업데이트가 가능한 방식입니다. Java로 되어 있습니다. 용도에 맞게 쓰려면 표현에 필요한 데이터 항목을 수정해야 하는데 그것 때문에 소스를 조금 수정해 주어야 합니다.
Libface 는 C++로 된 고속 대몬입니다. 써보진 않아서 아는 것이 별로 없습니다만 괜찮다고 합니다. 보기에도 괜찮아 보입니다.
이 외에도 몇개 더 있지만 소스가 오랫동안 개선 되지 않거나 사이트 자체가 사라져서 지금은 기억이 나지 않습니다.
검색엔진을 이용하는 방법
뭐 앞서의 방법이나 사실 다를바가 없지만 검색엔진 중에 자동완성 기능을 지원해주는 것들이 있습니다.
Elastic search도 기능을 지원합니다. 개발을 하지 않아도 되고 색인하는 방법만 익히면 쉽게 사용할 수 있습니다.
type-ahead 방식의 인메모리 자동완성 기능을 지원합니다. type-ahead방식은 뒤에 설명하겠습니다.
이 방법은 성능은 괜찮지만 다른 것에 비해서 무거운 검색엔진을 구동시켜야 한다는 부담이 있습니다. 하지만 대몬을 구동시키는 것이나 검색엔진을 구동시키는 것이나 데이터가 많아지면 부담스럽기는 매한가지입니다.
데이터 프로세싱
검색어 자동완성은 보통 두가지 데이터소스에서 데이터를 끌어와서 자동완성 대몬이나 서비스 구현체에 부어넣습니다.
- 로그
- 사용자가 입력한 검색어를 로그에 쌓아두고 빠르게 읽어서 자동완성 구동체에게 빠르게 공급합니다.
- 데이터베이스
- 상품의 이름을 쉽게 검색하게 하려는 쇼핑몰 같은데서는 굳이 로그를 뒤질 필요가 없습니다. 상품목록이나 주소, 사람이름 같은 것을 DB에서 내려받아 자동완성 구동체에 부어넣습니다.
로그를 읽어서 로그에서 많이 출현한 키워드에 가중치를 주거나 단순 횟수를 카운트해서 score값으로 쓸 수 있습니다. 로그를 추출할 때는 오타, 특수문자, 성인어 등을 어떻게 처리할지 함께 고민해야 합니다.
데이터베이스에서 꺼내 오는 경우는 상품명 같은것이 될텐데요. 검색어 자동완성도 일종의 추천시스템이라고 봐야하기 때문에 자동완성 목록을 추천할 때 단순히 가나다 순이 아닌 최신 상품이라든가 판매지수가 높은 상품이라든가를 상위에 노출되도록 하는 것을 고민해야합니다.
언어 처리
자동완성의 제안 목록이 되는 데이터를 프로세싱하고 대몬에 탑재할 때 고려할 것이 두가지 정도 더 있습니다.
형태소 분석기를 이용한 자동 띄어쓰기 및 자연어 처리
DB에 있는 상품명이든 사람들이 입력하는 키워드이던 띄어쓰기가 잘못되어 있는 경우가 있습니다. 이렇게 띄어쓰기가 잘 되어 있지 않은 것은 검색엔진에서 잘 다둬주지 않으면 제대로 된 검색결과를 리턴하지 않을 수 있습니다. 형태소 분석기에서 자동 띄어쓰기를 해서 잘 다듬어서 넣어주는 트릭이 필요할 수 있습니다.
자모분리
“빨간구두”를 키보드 한영전환을 하지 않고 두벌식으로 타이핑하면 “Qkfrksrnen”가 됩니다. 입력할 때 사용자가 영한전환을 안해서 생기는 문제인데 사용자의 실수라고 하더라도 “Qkfrks”를 치면 한글 “빨간…”으로 시작되는 검색어를 추천해서 사용자에게 편리함과 작은 감동을 주고 싶다면 데이터의 키를 만들 때 약간의 트릭을 쓰면 됩니다.
한글을 유니코드 처리를 이용해서 자모로 분리할 수 있고 자모에 대한 키보드상에 영문 매핑을 만든 후에 그것을 자료구조의 키로 만들어 주면 됩니다.
자판에서 ㄱ은 r에 매핑되고 ㄴ은 s에 매핑됩니다. 이렇게 변환된 것을 트리구조 또는 검색어 파편의 키로 만들어주면됩니다.
즉 “빨간구두”는 “Qkfrksrnen”를 키로 넣습니다.
대신 이 경우에는 Qkfrksrnen로 들어간 것이 원래 “빨간구두”였다는 것을 알아내야 하기 때문에 자료구조의 value에 함께 넣어두던가 역으로 복원하는 방법을 만들어 두어야 합니다. 번거롭긴 하지만 사용자 편의성을 높이는 방법 중 하나입니다.
위의 경우에 한글을 자모로 분리해서 영문키로 매핑하면 원래 영문으로 된 검색어는 어떻게 되는지 궁금하실지 모르겠습니다. 일부는 한글을 영타로 타이핑하면 영어에도 있는 단어와 겹치는 경우가 있지만 대부부의 경우는 겹치지 않습니다. 그래서 큰 문제는 안됩니다.
뒤로 매칭
“빨간”을 타이핑하면 “볼빨간”을 제안 즉 사용자가 입력한 키워드(입력하다만 키워드)로 끝나는 검색어를 추천해주고 싶을 수 있습니다.
사용자 자료를 찾기 위해서 키워드를 입력하는데 “빨간”은 생각이 나는데 이게 “볼빨간”인지 “눈빨간”, “목빨간” 인지 기억이 안날 수도 있습니다. 사용자를 잘 도와줘야 합니다.
이것은 간단한 방법을 쓰면 됩니다. 자료 구조에 데이터를 넣을 때 키의 문자열을 뒤집어서 넣으면 됩니다.
“볼빨간”을 자료구조에 넣을 때 “간빨볼”로도 하나 더 넣어두면 됩니다.
“볼빨간”이 영타로는 “qhfQkfrks”이기 때문에 다음처럼 해두면 됩니다.
키: value1, value2
qhfQkfrks: 볼빨간, 101
skrfkQfhq: 볼빨간, 100
위의 경우는 자료를 두벌 이상 넣어야 하기 때문에 대몬이 사용하는 메모리가 더 든다는 단점이 있습니다. 자료구조를 좀더 아름답게 고치면 메모리를 절약할 수도 있겠습니다.
런타임에 단어를 뒤집어서 조회를 해도 됩니다만 사용자의 키 타이핑이 빨라서 반응시간을 줄여야 하기 때문에 프로세싱할 때 미리 넣어두거나 대몬자체가 입력을 뒤집어서도 자료를 찾는 기능이 내장되어 있는 것이 좋습니다.
하지만 뒤집어서 넣는 것 보다는 type-ahead 방식이 여러모로 더 낫습니다.
그외 여러가지 잡다한 것들
자동완성은 영어로
- Auto-completion
- Auto type completion
- Type ahead search 또는 type ahead completion
- Completion suggest
다양 하게 부릅니다. 관련 영문 자료를 찾으시려면 저런 단어로 검색하시면 됩니다.
type-ahead 검색
type-ahead 검색은 auto-completion과 조금 구분이 되어야 합니다. type-ahead가 auto-completion의 일종이긴 하지만 단어의 어떤 부분을 매치해서 찾아주는지의 방법이 다소 다르기 때문입니다.
“검색어 자동완성” 이라는 키워드가 있고 사용자가 매치 되는 검색어의 일부를 타이핑했을 때 제안해 준다고 예를 들어 보겠습니다. 이때 n-gram 방식의 auto-completion과 type-ahead 방식의 차이로 인해서 제안 목록이 달라질 것입니다.
사용자 입력: “검색”
이때 제안할 검색어가 “검색”이라는 단어로 시작하기 때문에 두 방식다 제안이 됩니다.
사용자 입력: “자동”
이 경우에도 두 방식 모두 “검색어 자동완성”을 찾아서 제안해줍니다.
사용자 입력: “색어”
n-gram 방식은 찾아서 제안해 주지만 type-ahead 방식은 찾지 못합니다.
왜냐하면 type-ahead방식은 “검색어 자동완성” 이라는 검색어 제안을 공백을 기준으로 분리해서 앞에서부터 매치되는 것이 있는 것만 찾기 때문입니다. 최근의 검색어 자동완성이라고 하면 모두 type-ahead 방식을 말합니다. n-gram 방식이 효율도 좋지 않고 경우에 따라 제안되는 검색어가 다소 생뚱맞기 때문입니다.
type-ahead 방식을 트리 구조를 내장하고 있는 대몬에서 처리하게 하려면 key rotation이라는 간단한 트릭을 쓸 수도 있습니다.
아래와 같이 특별한 기호를 두고 공백을 기준으로 단어의 위치를 돌려서 모두 넣어준 다음에 찾을 때 찾고 보여줄 때는 원래 것을 보여주면 됩니다.
“검색어 자동 완성”
“자동|완성|검색어”
“완성|검색어|자동”
구현하려면 조금 번거롭기 때문에 오픈 소스들에는 대부분 type-ahead를 지원하기 때문에 특별히 다르게 구현해야 할 것이 아니라면 가져다가 그대로 쓰시는 것이 편할 것 같습니다.
데이터 분석
추가로 얘기하고 싶은 것은 사용자가 입력한 검색어를 데이터 분석의 목적으로 사용하는 것에 대한 것입니다.
사용자가 입력하는 키워드의 수을 세고 여러가지 정보를 붙여서 사용자들의 관심 동향(trend)를 보는 것을 하겠다고하면 검색키워드를 가지고 데이터 프로세싱을 한 후에 이것저거 살펴보고 이용하면 됩니다.
사실 이런 데이터를 들여다 보는 것은 매우 재미있습니다. 시간대와 사회적 이슈에 따라 입력하는 단어들의 경향이 달라지는 것을 볼 수 있으니까요.
하지만 자동완성이 붙어 있게 되면 몇가지 특별한 내용을 가리게 됩니다. 사용자가 어떤 키워드를 잘못 입력하지는 오타를 많이 입력하는지를 자동완성기능이 사용자의 입력을 유도해서 보이지 않게 만들 수 있습니다. 이런 경우에는 자동완성 대몬 자체가 로그를 남겨서 어떤 것들이 조회되는지 봐야 할 수 있고 자동완성의 frontend에서도 사용자가 검색어를 스스로 다 입력했는지 만약 자동완성제안 목록을 선택했다면 몇번째것을 선택했는지 등을 함께 로그에 남겨서 살펴봐야 합니다.