딥러닝 (Deep Learning)의 쉬운 이해
딥러닝은 “깊은 학습”이라는 뜻이고 “심화학습”이라고 번역합니다만 원래 뜻과는 잘 안맞고 멋이 없어서 그냥 “딥러닝”이라고 부릅니다.
딥러닝은 신경망(뉴럴 네트워크, Neural Network)이라고 하는 인공지능 구현 방식이 있는데 그 것의개량형입니다.
딥러닝은 신경망의 다른 별명이고 개량된 신경망을 뜻하는 단어입니다.
그래서 딥러닝을 이해하려면 신경망에 대해서 무조건 알아야 합니다.
신경망은 인간의 뇌구조를 모방해서 만든 인공지능을 만들기 위한 설계 구조이자 방식입니다.
신경망은 아주 예전에는 전기, 전자회로로 구현했고 요즘은 다 컴퓨터 소프트웨어로 구현합니다.
신경망을 개량하기 위해서 직접 만들기도 하고 기조의 구조를 고쳐서 인공지능 모델을 만들기도 합니다.
그래서 프로그래밍을 하긴하지만 프로그래밍 양은 많지 않고 만들어진 소프트웨어 골격을 재배열하고 데이터를 가공하거나 변환해서 넣고 결과를 확인하기 위한 것이 대부분입니다.
어쨌든 인공지능을 만들기 위한 절차의 집합입니다.
딥러닝과 일반 신경망의 차이
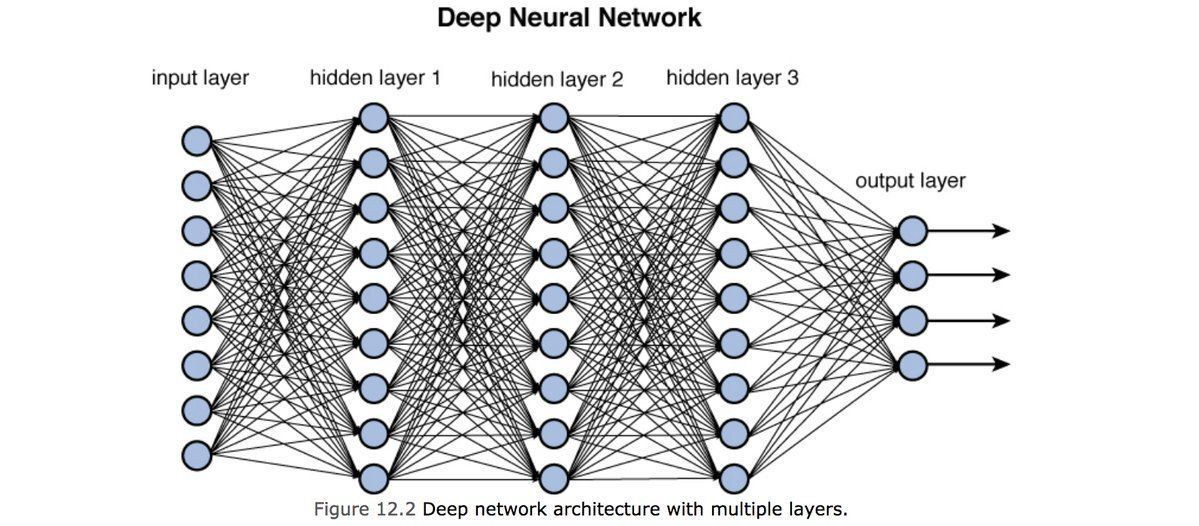
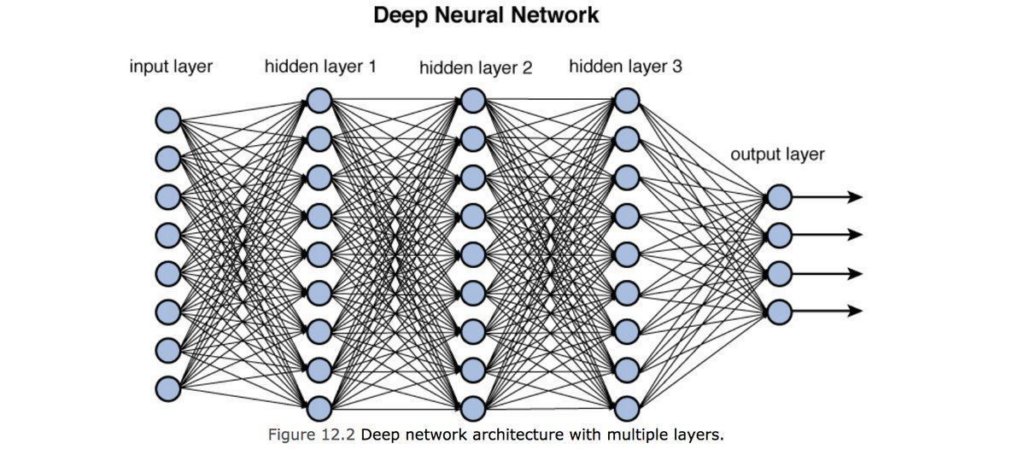
딥러닝과 일반 신경망의 차이는 딥러닝이 신경망의 구조에서 망 내의 신경 층들 수가 더 많고 길게 할 수 있다는 차이가 있습니다.
신경망이 깊으면 더 정교한 판단을 하는 인공지능을 만들 수 있습니다.
그럼 딥러닝이 나오기 전에는 깊은 구조 (복잡한 구조)의 신경망을 못 만들었다는 말인가? 라고 셩각하실텐데 그렇습니다.
딥러닝 이전에도 깊은 구조의 신경망을 만들 수는 있었지만 만들어진 신경망이 멍텅구리가 되기 때문에 결과적으로는 만들 수 없었습니다.
깊은 구조의 신경망을 만들 수 없었던 이유는 미분 때문
많은 이유가 있지만 가장 큰 이유는 미분으로 인한 문제입니다.
신경망에서 미분은 크게 2가지 문제를 만듭니다.
GPGPU로 대량의 계산을 더 빨리 처리하게 됨
신경망은 파라미터 최적화라는 작업을 합니다.
파라미터 최적화는 신경망 내에 있는 숫자값들을 학습데이터에 맞게 조금씨 고쳐서 바꿔가는 작업입니다.
파라미터 최적화를 위해서 대수학에서 하는 미분을 해야하는데 아주 많이해야 합니다.
미분을 많이해야 하면 계산할 것이 많아져서 컴퓨터가 힘이듭니다.
이건 이런 종류녜 단순 계산을 한 번에 많이 할 수 있는 GPGPU의 발전으로 해결되었습니다.
그래디언트 소실 문제 해결
그 다음은 미분이 반복되면서 파라미터의 숫자값들이 모두 0에 점점 가까워지는 문제를 해결했습니다.
이 문제를 그래디언트 배니싱이라고 부릅니다.
파라미터가 모두 0이 되거나 0에 가까우면 인공지능이 바보가 되는데 그 이유는 신경망의 층이 매우 많을 때 미분이 반복되기 때문입니다.
0이 가까워지는 이유는 미분의 대상이 되는 함수인 시그모이드라는 신경망에서 애용했던 함수의 특성때문입니다. 딥러닝에서는 이 함수를 렐루(ReLU)라는 미분해도 숫자가 계속 작아지지 않는 함수로 바꿔서 해결합니다.
알고보면 엄청 간단하지만 해결하는데 엄청나게 오랜 시간이 걸린 것입니다.
딥러닝 책과 자료는 서점과 온라인에 많이 있습니다. 자세한 자료는 그걸 참조하세요.