기여도
기여도란 어떤 성과지표에서 어떤 부분집합이 전체의 성과지표에 얼마나 형향을 주었는지 계산하는 것입니다. 리프트(lift)라고도 합니다. 리프트는 알고리즘이나 계산마다 각기 다르므로 일반적으로 말하는 리프트가 이것과 동일한 것은 아닙니다.
비율값이 지표인 경우에 총 지표를 만드는데 구성된 멤버 중 하나의 기여도가 얼마인지를 알아내는 간단한 함수입니다. 비율값이 아닌 지표에서의 기요도는 그냥 전체에서 해당 멤버가 차지하는 비중을 계산하면 되기 때문에 계산할 것이 없습니다.
비율값이 KPI인 경우를 예를 하나 들면 강고 배너 캠페인 5개를 운영하고 나서 전체 CTR과 각 배너별 CTR이 있을 때 배너별로 기여도를 계산하거나 하는 경우입니다.
비율값이 KPI인 경우에 기여도 계산이 어려운 이유
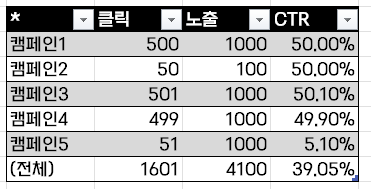
위의 표와 같은 5개의 캠페인이 있는데 클릭과 노출이 다 다릅니다. 이때 캠페인1과 캠페인2는 모두 CTR 0.5로 50%씩 동일합니다. 그런데 캠페인2는 캠페인1에 비해 노출과 클릭이 각각 모두 10배 많습니다.
상식적으로 생각할 때는 이런 경우 캠페인1이 기여도가 더 높아야 하는 것입니다.
기여도 계산에서 이것이 반영되야 합니다.
코드
코드는 R로 되어 있습니다. 하려고 했던 것은 calc_contrib_origin이라는 함수에서 계산할 때 분모가 0이 되는 문제로 기여도가 아예 계산이 안되는 것을 어떻게 해결할 것인가입니다.
이때 비율을 계산하는 것이기 때문에 분모가 0이 안되도록 하는 것이 중요한데 이 부분이 생각보다 까다롭습니다.
# 원래 함수
calc_contrib_origin <- function(total_z, total_c, z, c) {
((total_z / total_c) - ((total_z - z) / (total_c - c)))
}
# 멍청한 함수 v0
calc_contrib_mod1 <- function(total_z, total_c, z, c) {
frac <- total_c / c
((total_z / total_c) - ((z*frac) / (c*frac)))
}
# 멍청한 함수 v1
calc_contrib_mod1 <- function(total_v1, total_v2, v1, v2) {
frac1 <- total_v1 / total_v2
frac2 <- total_v2 / total_v1
if ((total_v1 == v1) && (total_v2 == v2)) {
cat("case 1\n")
(total_v1 / total_v2)
right <- 0
}
else if ((total_v1 != v1) && (total_v2 == v2)) {
cat("case 2\n")
(total_v1 / total_v2) - ((total_v1 - (frac2 * v1)) / v2)
right <- ((total_v1 - (frac2 * v1)) / v2)
}
else if ((total_v1 == v1) && (total_v2 != v2)) {
print("case 3\n")
(total_v1 / total_v2) - (v1 / (total_v2 - (v2 * frac1)))
right <- (v1 / (total_v2 - (v2 * frac1)))
} else { #
cat("case 4\n")
(total_v1 / total_v2) - ((total_v1 - v1) / (total_v2 - v2))
right <- ((total_v1 - v1) / (total_v2 - v2))
}
left <- (total_v1 / total_v2)
cat(paste0(left, " - ", right, "\n"))
return(left - right)
}
# 멍청한 함수 v2
calc_contrib_mod2 <- function(total_v1, total_v2, v1, v2) {
# frac1 <- total_v1 / v1
# frac2 <- total_v2 / v2
frac1 <- total_v1 / total_v2
frac2 <- total_v2 / total_v1
# 기준값
if ((total_v1 == v1) && (total_v2 == v2)) {
cat("case 1\n")
(total_v1 / total_v2)
right <- 0
}
# 분모가 0인 케이스
else if ((total_v1 != v1) && (total_v2 == v2)) {
cat("case 2\n")
#total_v1 / (total_v2 - v2)
right <- (v1 / (total_v2 - (v2 * frac1)))
}
# 분자가 0인 케이스
else if ((total_v1 == v1) && (total_v2 != v2)) {
print("case 3\n")
right <- total_v1 / (total_v2 - v2)
} else { #
cat("case 4\n")
(total_v1 / total_v2) - ((total_v1 - v1) / (total_v2 - v2))
right <- ((total_v1 - v1) / (total_v2 - v2))
}
left <- (total_v1 / total_v2)
cat(paste0(left, " - ", right, "\n"))
return(left - right)
}
# 덜 멍청한 함수 v1
calc_contrib_mod1 <- function(total_z, total_c, z, c) {
(((total_z + 1) / (total_c + 1)) - ((total_z - z + 1) / (total_c - c + 1)))
}
# 덜 멍청한 함수 v2
calc_contrib_mod2 <- function(total_z, total_c, z, c) {
lb <- 1 - 1 / (total_c + 1)
rb <- 1 - (total_z + 1) / 1
print(c(lb, rb, rb - lb))
( (((total_z + 1) / (total_c + 1)) - ((total_z - z + 1) / (total_c - c + 1))) ) / (rb - lb)
}
calc_contrib_mod <- calc_contrib_mod1
# ※ 전체 비율에서 항목값들이 존재하지 않았을 경우를 계산하는 것이 전부
# ※ 따라서 전체 비율을 계산하고 대상 항목의 수치를 포함하지 않은 것의 비율을 계산해서 뺀다
# 간단한 테스트
calc_contrib_mod(50, 100, 49, 60)
calc_contrib_mod(50, 100, 50, 60)
calc_contrib_mod(50, 100, 50, 59)
# 계산검증1. (o)
calc_contrib_mod(200, 250, 202, 250) # 아래 보다는 높아야 함 (o)
calc_contrib_mod(200, 250, 201, 250) # 아래 보다는 높아야 함 (o)
calc_contrib_mod(200, 250, 200, 250) # 기여도 100% (기준 기여도와 동일) (o)
calc_contrib_mod(200, 250, 199, 250) # 위의 것 보다는 낮아야 함 (o)
calc_contrib_mod(200, 250, 198, 250) # 위의 것 보다는 낮아야 함 (o)
calc_contrib_mod1(200, 250, 200, 0)
# 계산검증1-1 (o)
calc_contrib_mod(200, 250, 101, 50) # 아래 것 보다는 높아야 함 (o)
calc_contrib_mod(200, 250, 100, 50) # 아래 것 보다는 높아야 함 (o)
calc_contrib_mod(200, 250, 100, 51) # 위의 것 보다 낮아야 함 (o)
# 계산검증2 (o)
calc_contrib_mod(250, 200, 251, 200) # 기준기여도 보다 높거나 같아야 함
calc_contrib_mod(250, 200, 250, 200) # 기여도 100% (기준 기여도와 동일)
calc_contrib_mod(250, 200, 249, 200) # 위의 것 보다 낮아야 함 (o)
calc_contrib_mod(250, 200, 248, 200) # 위의 것 보다 낮아야 함 (o)
calc_contrib_mod(250, 200, 247, 200) # 위의 것 보다 낮아야 함 (o)
# 계산검증3 (o) 점진적으로 높아지는
calc_contrib_mod(250, 200, 50, 100)
calc_contrib_mod(250, 200, 100, 100)
calc_contrib_mod(250, 200, 100, 50)
calc_contrib_mod(250, 200, 100, 2)
calc_contrib_mod(250, 200, 100, 1)
# 계산검증4 (o) 점진적으로 낮아지는
calc_contrib_mod(250, 200, 100, 1)
calc_contrib_mod(250, 200, 100, 2)
calc_contrib_mod(250, 200, 100, 99)
calc_contrib_mod(250, 200, 100, 100)
calc_contrib_mod(250, 200, 100, 101)
calc_contrib_mod(250, 200, 100, 102)
# 계산검증5 (o). 다운 방향으로 기여도가 떨어져야함
calc_contrib_mod(110, 110, 100, 1)
calc_contrib_mod(110, 110, 100, 2)
calc_contrib_mod(110, 110, 100, 99)
calc_contrib_mod(110, 110, 100, 100)
calc_contrib_mod(110, 110, 100, 101)
calc_contrib_mod(110, 110, 100, 102)
# 계산검증6 (오류)
calc_contrib_mod(110, 110, 110, 1) # 아래것 보다 좋음 (o)
calc_contrib_mod(110, 110, 110, 2) # 아래것 보다 좋음 (o)
calc_contrib_mod(110, 110, 110, 99) # 아래것 보다 좋음 (o)
calc_contrib_mod(110, 110, 110, 100) # 아래것 보다 좋음 (o)
calc_contrib_mod(110, 110, 110, 101) # 아래것 보다 좋음 (o)
calc_contrib_mod(110, 110, 110, 102) # 아래것 보다 좋음 (o)
calc_contrib_mod(110, 110, 110, 109) # 아래것 보다 좋음 (x)
calc_contrib_mod(110, 110, 110, 110) # 기준
calc_contrib_mod(110, 110, 109, 109)
calc_contrib_mod(110, 110, 108, 108)
calc_contrib_mod(110, 110, 110, 111) # ※ 입력이 잘못된 케이스.
calc_contrib_mod(110, 110, 110, 112) # ※ 입력이 잘못된 케이스.
# 계산검증7 (x)
# 항목값이 가분수가 되면 결과값이 마이너스가 되는데
# 이것들이 기준값과 진분수인값들과 차이가 생긴다.
calc_contrib_mod(210, 110, 110, 1) # 아래것 보다 좋음 (o)
calc_contrib_mod(210, 110, 110, 2) # 아래것 보다 좋음 (o)
calc_contrib_mod(210, 110, 110, 99) # 아래것 보다 좋음 (o)
calc_contrib_mod(210, 110, 110, 100) # 아래것 보다 좋음 (o)
calc_contrib_mod(210, 110, 110, 101) # 아래것 보다 좋음 (o)
calc_contrib_mod(210, 110, 110, 102) # 아래것 보다 좋음 (o)
calc_contrib_mod(210, 110, 110, 109) # 아래것 보다 좋음 (x)
calc_contrib_mod(210, 110, 110, 110)
calc_contrib_mod(210, 110, 100, 110) # 위 보다는 안좋음
calc_contrib_mod(210, 110, 1, 110) # 위 보다는 안좋음
# -- 비교 (origin함수) (x)
calc_contrib_origin(210, 110, 110, 1) # 아래것 보다 좋음 (o)
calc_contrib_origin(210, 110, 110, 2) # 아래것 보다 좋음 (o)
calc_contrib_origin(210, 110, 110, 99) # 아래것 보다 좋음 (o)
calc_contrib_origin(210, 110, 110, 100) # 아래것 보다 좋음 (o)
calc_contrib_origin(210, 110, 110, 101) # 아래것 보다 좋음 (o)
calc_contrib_origin(210, 110, 110, 102) # 아래것 보다 좋음 (o)
calc_contrib_origin(210, 110, 110, 109) # 아래것 보다 좋음 (x)
calc_contrib_origin(210, 110, 110, 110)
calc_contrib_origin(210, 110, 100, 110) # 위 보다는 안좋음
calc_contrib_origin(210, 110, 1, 110) # 위 보다는 안좋음
# 계산검증8. (o)
calc_contrib_mod(110, 210, 1, 110)
calc_contrib_mod(110, 210, 109, 110) # 위 보다는 좋음
calc_contrib_mod(110, 210, 110, 110) # 위 보다는 좋음
# origin 함수 확인
calc_contrib_origin(110, 210, 109, 110) # 위 보다는 좋음
calc_contrib_origin(110, 210, 110, 110) # 위 보다는 좋음
# 심1
calc_contrib_origin(110, 210, 109, 110)
calc_contrib_origin(210, 110, 110, 109)
# 산수 노트
at <- 50
bt <- 100
a <- 30
b <- 15
(at / bt) - ((at - a) / (bt - b))
(at / bt) - ((at - a) * (bt - b)^-1)
(2 - 3)^2
2^2 + -2*(2*3) + 3^2
(2 - 3)^-1
# a²-2ab+b² = (a-b)²