삼각함수와 선형대수학에 대한 기본적인 배경지식이 있다면 코사인 유사도는 이해하기 매우 쉽습니다. 그게 아니라면 처음에 개념을 잡는 것이 어려울 수 있습니다. 그렇다고해서 겁 낼 필요는 전혀 없습니다. 어마무지하게 어려운것이 아니라서 포기하지 않고 조금 신경쓰고 조금 시간을 쓰면 누구나 이해할 수 있는 것입니다.
이 글에 대해서
이 글은 조금 쉽게 풀어서 설명하려다 보니 내용이 조금(많이) 길게 되었습니다. 그러니 만약 이 글을 읽을 것이라면 시간적 여유가 있을 때 보시면 좋겠습니다. 보통 코사인 유사도는 교과서에서 매우 간단하게 설명하고 넘어가는데 그건 다 알고 있다는 가정에서 설명하기 때문입니다. 이것은 문제가 있는데 보는 사람은 모르기 때문에 교과서를 보는데 아는 것을 가정하고 간단하게 설명한다는 것은 매우 이상합니다. 어쨌든 그런 부분까지 쉽게 풀어서 쓰다 보니 글이 장황해 졌습니다. 제 탓입니다.
코사인유사도는 대체 뭘까?
우선 개념(concept) 이해를 위해서 코사인유사도를 아주 짧게 정의해서 설명하면 이렇습니다.
두 벡터(Vector)의 사잇각을 구해서 유사도(Similarity)로 사용하는 것
혹시 벡터라는 용어에 울렁증이 있더라도 여기에서 포기하지마세요. 별거 아닙니다.
여기서 유사도를 구할 때 두 벡터 사이의 각을 코사인(Cosine)값으로 구해서 유사도값으로 사용하기 때문에 코사인 유사도(Cosine Similarity)라고 부릅니다. 더 줄여서 말하면 두 벡터의 사잇각을 코사인으로 구하면 되는 것입니다.
수포자라면 아직도 이 설명 자체로는 이해가 어렵겠습니다만 괜찮습니다. 좀더 읽어 보세요.
코사인이 나왔으니 말인데 코사인 외에도 삼각함수에서 늘 같이 딸려 나오는 사인(Sine)이나 탄젠트(Tangent)로 값을 계산했다면 아마 “사인 유사도”나 “탄젠트 유사도”로 불렀을 것입니다만, 굳이 코사인을 사용한 것은 이런 계산을 하는데 코사인값으로 계산하는 것이 더 쉽고 편하기 때문입니다. 코사인으로 계산하면 계산을 덜 해요. 그것 뿐입니다.
벡터의 유사도를 구하는 방법은 여러가지가 있습니다. 코사인 유사도는 그 중 하나입니다. 다른 것과는 다르게 코사인 유사도의 특징은 사잇각을 쓴다는 것입니다.
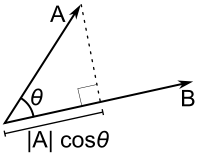
저 위에 설명을 위한 매우 간단한 삼각형 그림이 있습니다. 코사인 유사도를 설명하는 문서에서 예제로 많이 보여주는 매우 흔하고 유명한 그림입니다.
저 그림을 보고 설명하면 그림에서 A와 B는 유사도를 계산할 대상이 되는 두 벡터(vector, 또는 두개의 수열값 세트)이고 두 벡터의 A와 B의 사잇각 쎄타를 코사인으로 구하는 것이고 구해진 사잇각의 값을 코사인 유사도로 사용하는 것입니다.
여기에서 각이란 원점에서 각 벡터의 위치까지 선으로 이어서 선을 만든 다음 두 선의 각을 말하는 것입니다. 원점은 모든 좌표의 값이 0이 되는 곳입니다. 이건 수학시간에 배우셨지요?
벡터는 무엇인가?
이 지면에서 벡터까지 설명해야 하는 것은 너무 길어서 무리이겠지만 그래도 벡터에 대해 익숙하지 않은 분들을 위해서 먼저 벡터에 대해서 간단히 설명을 하고 넘어가겠습니다. 이미 잘 아신다면 당연히 이 부분은 건너 뛰어도 됩니다.
위의 그림에서 두 벡터는 2차원 벡터를 표현해 놓은 것입니다. 그림은 가로와 세로로 축이 2개있는 평면이니까요. 축이 2개라서 숫자도 2개씩입니다.
벡터는 2차원 이상의 고차원 벡터도 있습니다. 현실의 데이터는 대부분 수십차원에서 수백만차원까지 가는 고차원 벡터를 다루는 일이 더 많습니다. 숫자 2개가지고는 뭐 할 수 있는 것이 별로 없습니다. 정보량도 적구요. 고차원 벡터는 그림에서 보이는 x축, y축과 같은 축들이 더 많다고 생각하면 됩니다. z, l, m, n, … 등으로 말이지요.
벡터의 차원에 대해서 잠깐 설명하고 넘어가면 예를 만들어 보면 10차원 벡터는 아래와 같습니다.
10차원의 두 벡터의 예:
- A = 1,2,3,4,5,6,7,8,9,10
- B = 2,3,4,5,6,7,8,9,10,11
A와 B는 각각 수열(수의 나열)이고 각각 10개씩 숫자를 가지고 있으므로 둘 다 10차원의 벡터입니다. 앞서 말씀드렸듯이 10차원 벡터는 눈으로 볼 수 있게 시각적으로 표현할 수 없습니다. 삼각형이나 선으로 좌표축에 그릴 수 없습니다.
수학 수업에서 배우기도 하는데 배우셨더라도 아마 잊어버렸겠지만 3차원까지는 시각적으로 표현이 가능하지만 4차원부터는 인간의 눈으로 한 눈에 볼 수 있게 시각적으로 표현하는 것은 불가능합니다. 인간이 통제할 수 있는 차원이 3차원까지만 가능하기 때문입니다. 그 이상은 머리속으로 추상적으로만 연상(imagination)을 해야 합니다. 이건 아인슈타인도 못 그립니다.
어쨌든 10차원 보다 숫자들이 하나씩 더 있으면 11차원이고 1000개가 되면 1000차원입니다. 그냥 각 축에서 위치를 나타내는 숫자가 1000개 있으면 1000차원 벡터, 10000개면 10000차원 벡터입니다.
물론 여러 벡터가 있다면 각 벡터에서 숫자의 순서들은 서로 같은 의미를 가지는 것에서 가져온 숫자여야 합니다. 이것 마저 설명하면 매우 복잡해지니 여기서는 그냥 잊어버리셔도 됩니다.
2차원이든 100차원이든 1000차원이든 시각적으로 표현이 불가해도 코사인 유사도는 정해진 공식으로 구할 수 있고 구하는 방법도 간단합니다.
코사인 유사도의 용도
계산법을 보기전에 아마도 많은 분들이 궁금할 것이 “두 벡터의 유사도를 구해서 어디에 쓰는가?” 라는 것일텐데요. 용도를 알게 되면 이해하는 것이 더 쉽습니다.
그런데 그전에 또 먼저, 벡터의 유사도는 무엇인가?
용도를 설명하기 전에 유사도를 먼저 설명해야 합니다. 그 참 설명을 하기위해서 먼저 설명해야할 뭔가가 정말 많습니다만. 벡터의 유사도를 구하는 것은 비슷하다는 것을 어떻게 정의하냐에 따라 계산하는 방법이나 결과들이 마구 달라집니다. 우선 벡터는 그냥 숫자들의 묶음이라고 생각해보면 이것만으로는 무작정 비슷한지 아닌지를 알 수 없는 문제도 있습니다.
유사도를 직선거리(유클리디안 디스턴스; euclidean distance)로 구하거나 사잇각이 얼마나 좁은지를 계산해서 구하거나 하는 것이 가장 잘 알려진 것입니다. 사잇각을 계산해서 유사도를 구하는 것 중에 가장 잘 알려진 것이 코사인 유사도입니다.
또 고등학교 수학책을 보면 두 벡터의 내각을 구하는 것으로 코사인 유사도가 이미 나와있습니다. 아마도 배웠지만 잊어 버린 사람들이 많을 것입니다.
코사인 유사도의 용도
코사인 유사도는 대충 다음과 같은 구체적인 용도가 있습니다. 흔히 볼 수 있는 것들입니다.
- 검색 엔진에서 검색어(Query)와 문서(Document)의 유사도를 구해서 가장 유사도가 높은 것을 먼저 보여주기 위한 기본 랭킹 을 위한 알고리즘으로 사용됩니다.
- 텍스트마이닝에서 쓰입니다. 검색엔진과 텍스트마이닝이 상당히 관련이 있기 때문에 사실 1번과 관련성이 깊습니다. 텍스트 마이닝은 흔히 벡터 스페이스 모델(Vector Space Model)을 사용하고 TF-IDF(Term Frequency – Inverse Document Frequency)를 사용하는데 단어집합들 간의 유사도를 구하기 위해서 코사인 유사도를 사용하는 것이 빈번하게 나옵니다. 그래서 word2vec 같은 딥러닝 모델에서도 나옵니다.
- 그 외에도 다른 분석이나 수리 모형에서도 유사도를 구할 때 사용합니다. 가끔 나옵니다. 매우 빈번하게 사용하지는 않습니다.
- 클러스터링(Clustering, 군집화) . 군집화 모델에서 데이터 포인트를 서로 묶을 때 쓰이긴 합니다.
위의 예에 대해서 부연설명을 더 해보겠습니다. 역시 매우 장황하니 관심 없으시면 건너 뛰셔도 됩니다.
*위의 1번의 검색 랭킹의 문제*
검색엔진이나 텍스트 마이닝에서 주로 쓰이는 이유는 문서를 숫자로 표현하는 방법중에 가장 쉽고 잘 알려진 방법이 포함된 단어들의 출현 횟수를 세고 그걸 숫자로 만드는 것이기 때문입니다.
검색엔진에서 흔히 비교할 문서들은 검색엔진의 검색창에 입력한 질의어(query라고 합니다)와 검색엔진이 가지고 있는 문서들을 비교해서 가장 비슷한 것을 찾기 때문입니다. 여기서 코사인 유사도를 구하는 대상이 사용자가 입력한 질의어와 검색엔진이 가지고 있는 모든 문서들과의 쌍입니다. 그렇게 해서 코사인 유사도를 구해서 가장 유사도가 큰 것을 가장 위에 보여줍니다. (현재의 검색엔진은 이렇게 단순하게 작동하지 않습니다. 오해를 방지하기 위해서 적어둡니다).
이때 검색엔진이나 텍스트마이닝에서는 유사도를 비교할 때 단순히 단어의 출현횟수만을 가지고 문서를 수치데이터(벡터)로 바꾸지 않고 TFIDF라는 수치값을 계산해서 씁니다. 그래서 코사인유사도와TFIDF는 늘 쌍으로 같이 언급이 됩니다. 이건 나중에 기회가 되면 설명하겠습니다. (TFIDF에 대한 포스트를 참고하세요)
*위의 3번의 클러스터링에서의 문제*
클러스터링에서의 거리 계산은 모두 연산 자원(Computational Cost) 문제와 관련이 있습니다. 코사인 유사도 역시 그렇습니다.
유사도를 구하는 목적의 근본적인 목적이 $latex A$가 $latex B$와 유사한지 $latex A$와 $latex C$가 더 유사한지와 같은 상대적인 비교를 하기 위한 것입니다.
A와 B가 둘만 있다면 둘을 비교해서 둘이 얼마나 유사한지는 사실 알 수 없습니다. 알 필요도 없습니다.
예를들어 세상에 사람이 둘 만 남았다면 이 두 사람은 서로 가장 비슷하게 생긴 사람일까요? 아니면 서로 전혀 다른 사람일까요? 두가지 모두 해당되기도 하겠지만 실제는 이게 쓸모가 없습니다. 그냥 모르는 것입니다.
즉 A와B, C, …등등이 있으면 가장 유사한 것들끼리 묶어보거나 A와 가장 비슷한것을 B, C 와 같은 것 중에서 찾아서 고르는 경우가 대부분이기 때문입니다. 그래서 여러 개의 벡터를 대상으로 각각 서로 서로 쌍을 맺어 유사도를 구해서 가장 유사도가 높은 순으로 정렬해서 가까운 것 1개를 선택한다거나 여러개를 선택해서 여러가지 목적으로 사용하게 됩니다.
클러스터링을 할 때도 마찬가지겠지요 벡터의 개수 즉, 비교할 데이터가 $latex n$개고 벡터로 표현할 수 있다면 $latex \frac{n \times (n-1) }{2}$번 만큼 연산을 해야 합니다. RDMBS에 100개의 레코드가 있고 컬럼이 여러개 있는데 모두 숫자라면 각 레코드들 간의 유사도를 모두 구하면 $latex \frac{100(100-1)}{2}$ 만큼 유사도값을 뽑아야 합니다. 에… 계산하면 4950번 입니다.
코사인 유사도를 위한 전제 조건
매우 기본이 되는 것이라 설명을 할 필요가 없겠지만 이왕 이 글이 너무 장황해진 김에 적어 보자면 다음과 같은 전제 조건이 있습니다.
- 두 벡터의 원소들은 모두 양수(플러스!)여야 합니다. x, y 직교 좌표축에서 1사분면에 오는 것들입니다. (모눈종이에서 중심을 기준으로 오른쪽 위)
그래서 원소들의 값이 음수가 되지 않는 문제에만 가져다 씁니다. - 벡터의 원소수는 같아야 합니다.
너무 당연한 것입니다. 비교하는 벡터의 원소 갯수가 일치하지 않으면 각각 빠진 것을 0으로 채워서 동일하게 만들어야 합니다. 벡터의 원소 갯수가 좌표축에서의 축의 갯수이기 때문입니다.
코사인 유사도의 특징
평면 좌표에서 1사분면의 두 벡터의 코사인 값은 0 ~ 1 사이의 값입니다. 벡터의 각이 작을 수록 1에 가까워지고 클수록 0에 가까워집니다. 따라서 결과를 재가공(rescaling)하지 않고 바로 쓰기 편합니다. 두 벡터가 정확히 직교이면 값이 0이 됩니다.
삼각함수를 배울 때 이미 배우는 것이기 때문에 이걸 기억 하고 있다면 좋겠습니다만 생각하지 않는다면 다시 한 번 찾아보세요.
공식
공식입니다. 자세히 보지 마세요.
$latex \text{similarity} = cos(\theta) = {A \cdot B \over |A| |B|} = \frac{ \sum\limits_{i=1}^{n}{A_i \times B_i} }{ \sqrt{\sum\limits_{i=1}^{n}{(A_i)^2}} \times \sqrt{\sum\limits_{i=1}^{n}{(B_i)^2}} }$
아주 간단한 공식이고 고등학교 수학교과서에도 나옵니다. 공식은 매우 쉽기 때문에 한 번 이해를 하고 나면 볼 필요도 없습니다.
공식 풀이
공식을 가능한 자세히 설명을 적어 보겠습니다. 먼저 공식에서 분자 부분과 분모 부분을 나눠서 설명하면 다음과 같습니다.
분자 부분 – 벡터 내적 (vector inner product, dot product)
코사인 유사도 공식에서의 분자 부분은 벡터의 내적(dot product)을 구하는 것입니다. 영어로는 inner product(이너 프러덕) 또는 dot product(닷프러덕)이라고 흔히 말합니다.
$latex \ll A \cdot B \gg $이 벡터의 내적(dot product) 표기입니다.
벡터의 내적은 계산이 매우 쉽습니다.
두 벡터의 각 원소들을 순서대로 짝맞춰서 곱한 다음에 결과들을 다 더하면 됩니다.
아래와 같은 두 벡터가 있다고 하겠습니다. 차원이 5차원인 2개의 벡터입니다. 요소가 5개이기 때문에 5차원입니다. (외계인이 산다는 그 5차원이 아닙니다) 값은 현실의 예제가 아닌 제가 임의로 마구 넣은 것입니다.
$latex A = (1,2,3,4,5) $
$latex B = (6,7,8,9,10) $
- 각각 짝을 지어 잘 곱합니다. 순서를 맞춰서 잘 해줍니다.
$latex 1 \times 6 = 6$
$latex 2 \times 7 = 14$
$latex 3 \times 8 = 24$
$latex 4 \times 9 = 36$
$latex 5 \times 10 = 50$ - 곱한 것을 다 더합니다.
$latex 6 + 14 + 24 + 36 + 50 = 130$
위의 과정이 벡터의 내적을 구한 것입니다.
끝입니다. 너무 힘든 계산이었습니다. 썰렁한 농담입니다.
그런데 여기서 벡터의 내적이 왜 나오는지 궁금할 수 있습니다. 각을 구하는데 왜 저런게 필요한 것이지? 이것은 뒤에 설명하겠습니다.
분모 부분 – 두 벡터의 크기를 곱한다
분모 부분은 두 벡터의 크기를 각각 구해서 곱하면 됩니다.
$latex |A|$는 A벡터의 크기를 말합니다.
$latex |B|$는 B벡터의 크기를 말합니다.
분모는 두벡터의 크기를 구해서 곱하면 되는데요 벡터의 크기(norm 이라고 부릅니다)가 기억이 안나실 수 있는데요. 원점에서부터의 거리를 말하는데. 이건 기하학적으로 보면 사실 ‘피타고라스 정리‘에서 직각삼각형의 빗변을 구하는 것을 말합니다.
그냥 “피타고라스 정리를 이용해서 빗변을 구하는 것을 하면된다”는 말입니다.
그런데 2차원까지는 직각삼각형인데 3차원부터는 입체가 되고 4차원부터는 아예 모양을 상상도 할 수 없게 됩니다만 그래도 피타고라스 정리로 구할 수 있다고 수학자들이 증명을 이미 해놓았습니다. 믿고 쓰면 됩니다. 못 믿으시겠으면 직접 증명을 해보시면 됩니다.
자! 앞에서 설명했듯이 벡터의 길이는 피타고라스 정리를 사용하면 구할 수 있고 그걸로 2개의 값을 구해서 서로 곱하면 분모 부분은 완성됩니다.
직각삼각형의 빗변의 길이를 구하는 피타고라스 정리를 기억 못하면 매우 곤란합니다.
$latex C=\sqrt{ A^2 + B^2 }$
- A벡터의 크기를 구합니다. 피타고라스 정리.
$latex \sqrt{ 1^2 + 2^2 + 3^2 + 4^2 + 5^2 } = 7.4161984870957$
- B벡터의 크기를 구합니다. 피타고라스 정리.
$latex \sqrt{6^2 + 7^2 + 8^2 + 9^2 + 10^2} = 18.1659021245849$
- 이제 마무리로 구한 것을 곱합니다
$latex 7.4161984870957 \times 18.1659021245849 = 134.7219358530751$
숫자값들이 소숫점 뒤로 길게 나와서 복잡해 보이지만 별거 아닙니다. 뭐 계산은 계산기나 컴퓨터가 하는 거니까요.
마무리 계산 – 분자를 분모로 나누기
이제 다 구했으니 분자를 분모로 나눕니다. 나누기는 매우 힘든 산술계산이지만 우리에게는 계산기가 있습니다.
$latex \frac{130}{134.7219358530751}=0.9649505$
위에 계산된 결과 값이 코사인 유사도 값입니다. 약 0.96이네요.
풀어놓고 보니 별거 아닙니다.
R 코드로 풀어보면 이렇습니다.
# 벡터가 둘이 있습니다.
vector1 <- c(1, 2, 3, 4, 5)
vector2 <- c(6, 7, 8, 9, 10)
# 그냥 구하기 (코드를 더 짧게 줄일 수도 있습니다만)
numer <- sum(vector1 * vector2)
denom <- sqrt(sum(vector1^2)) * sqrt(sum(vector2^2))
numer / denom
# lsa 패키지에서 제공하는 펑션으로 구하기
install.packages("lsa")
library(lsa)
cosine(vector1, vector2)
R도 되지만 Pyhon이나 다른 언어들로도 당연히 계산이 됩니다. 엑셀도 됩니다. 그리고 위의 코드에도 나와 있지만 특별한 경우가 아니라면 굳이 계산식을 따로 코딩으로 구현할 필요는 없습니다. 대부분 소프트웨어 내에서 자체 제공하거나 컴퓨터 언어들의 추가 패키지, 라이브러리로 제공하고 있어서 매우 쉽게 계산이 가능합니다.
여기에서 벡터 내적은 왜 나오는 것일까?
내적에서 무너질 분들이 좀 있을텐데요. 고교 수학에 분명 나옵니다. 기억 안나도 괜찮습니다. 어차피 이것도 설명할꺼니까요.
벡터의 내적은 검색을 해 보시면 자료가 많이 나올 것입니다. 수학적으로 매우 중요한 것 중 하나입니다. 특히 선형대수학은 벡터의 내적이 없으면 있으나 마나한 물건이 됩니다. 사실 코사인 유사도를 이해못하는 대부분의 이유는 내적을 이해하지 못하기 때문입니다.
위의 삼각형 그림을 다시 살펴보면 코사인 법칙은 피타고라스 정리에서 출발했기 때문에 코사인값을 구하려면 두 벡터가 만드는 내부의 도형이 직각삼각형이어야 합니다. 그런데 위의 그림을 보시면 A, B와 원점이 만드는 도형이 직각삼각형이 아닌 것을 알 수 있습니다. 그냥 삼각형입니다. 하다 보면 저런 삼각형이 운이 좋게 직각삼각형인 경우도 있겠지만 매우 드물고 요행으로 “직각삼각형이 될지어다!” 라고 바라는 것은 일반화된 해결책이 아니기 때문에 의미가 없습니다.
직각삼각형이 되는 것은 위의 그림에서는 |A|와 B와 원점으로 만든 삼각형입니다. 직각 표시 보이시죠? 그래서 직각삼각형으로 만들어서 피타고라스 정리에서 출발한 코사인 법칙으로 사잇각을 계산하려면 |A|의 길이를 알아내야만 합니다.
이 |A|의 길이를 알아내는 방법이 벡터의 내적을 이용하는 것입니다.
A와 B의 두 벡터가 있을 때 A와 B의 내적을 계산하면 B * |A| 또는 A * |B|를 구할 수 있습니다.
여기서 |A|는 A를 B의 벡터의 선상(또는 연장선상)으로 직교(직각)이 되게 그대로 내린(정사영 영어로는 projection 한다고 표현합니다) 곳과 원점까지의 거리입니다. |B|는 반대편으로 B를 정사영 한 것입니다.
B 곱하기 |A| = |B| 곱하기 A
정사영을 어느 쪽으로 하던지 상관없습니다. 두 값은 항상 동일합니다. 왜 동일한지까지 설명하려면 지면이 너무 많이 필요해서 생략하겠습니다. (곰곰히 생각해 보면 같을 수 밖에 없다는 것을 알 수 있습니다)
네. 두 벡터의 내적값은 항상 1개입니다. 어느 방향으로 구해도 똑 같습니다.
결국 두 벡터의 내적을 구해서 벡터 하나의 크기로 나누면 |A| 또는 |B|의 길이를 구할 수 있어서 저 상황에서 직각삼각형을 만들 수 있습니다. 더 정확하게 말하면 직각삼각형을 이루는 구성요소인 세 변을 모두 찾아 낼 수 있습니다.그러면 비로서 코사인값을 계산할 수 있게 됩니다.
간단한 요약
벡터의 내적은 왜 필요하냐?
두 벡터 사이에 있는 직각삼각형때문에요.
직각삼각형은 왜 나오냐?
코사인값을 구해야 해서요.
코사인값이 직각삼각형과 무슨 관계냐?
코사인법칙이 피타고라스 정리에서 나왔기 때문에요.
그래서 두 벡터가 유사한지 어떻게 알 수 있는가?
이름이 코사인 유사도이니 이것의 용도가 어떤것이 유사한지 아닌지를 확인하는 것이라는것은 유추할 수 있는데 두 개의 벡터만으로는 서로 유사한지 아닌지를 알기 어렵습니다. 아니 모릅니다. 유사한지 아닌지와 가까운지 먼지 판단하는 기준은 상대적인 것입니다. 물론 절대적인 기준값을 하나 정해놓고 유사하다 아니다를 결정하는데 사용해도 됩니다. 하지만 그 기준값을 또 직접 결정해서 만들어줘야하고 적당히 좋은 값을 정하기가 더 어렵습니다.
위에서 잠깐 설명했지만 코사인의 특징으로 두 벡터의 각이 호도법으로 0도가 되면 코사인 유사도값은 1이되고 호도법으로 각이 커질수록(90도에 가까워 질수록) 0에 가까워진다는 것입니다. 조금 풀어서 설명하면 코사인유사도가 0 또는 Inf가 되면 전혀 유사하지 않은 직교(orthogonal)가 되고 1이 되면 두 벡터의 원점으로부터의 방향이 완전히 겹치게 됩니다. 그런데 이것만으로는 유사한지 아닌지를 판단하기 어렵습니다. 호도법으로 45도 보다 각이 작으면 유사하다고 해야 할까요?
유사도는 상대적인 개념이기 때문에 벡터 2개로는 두 벡터가 유사한지 아닌지를 알기는 어렵습니다. 벡터가 최소 3개 이상은 있어야 합니다.
그래서 N개의 벡터가 있고 A라는 1개의 벡터가 있을때 A벡터와 가장 가까운 벡터를 N개 중에서 찾을 때 코사인 유사도를 사용해서 코사인 값이 가장 큰 것을 선택해서 사용합니다. 당연히 코사인값은 N번 계산해야 합니다.
A벡터가 상대적으로 가장 가까운 벡터는 어떤 것인가를 찾는 것입니다.
어째서 두 벡터의 직선 거리를 계산하지 않고 각도를 사용하는가?
두 벡터가 가까운지 아닌지를 찾는 방법중에 가장 쉬운 것이 직선거리를 계산하는 유클리디안 거리(Euclidean distance)입니다. 유클리디안 거리의 문제점은 각 축의 숫자값의 크기에 따라 영향을 크게 받는다는 것입니다. 축이 수량값을 나타내는 것이고 각축의 값들이 매우 큰 벡터들가 매우 적은 벡터들이 섞여 있다면 벡터의 성향보다는 양적수치가 비슷한 벡터끼리 가깝게 계산되는 경우가 많습니다.
물론 이것도 나름대로 의미가 있기 때문에 이 자체로 큰 문제가 있는 것은 아닙니다. 하지만 양적 크기가 차이 클 것이 뻔한 데이터들은 유클리디안 거리를 사용하면 대부분 문제가 있습니다.
적용하려는 데이터의 특징과 사용하는 사람의 의도에 맞는 것을 선택하면 되는 것입니다.
텍스트마이닝에서의 코사인 유사도
앞서에서도 잠깐 설명을 했지만 코사인 유사도는 텍스트 데이터(텍스트 마이닝)에 사용하는 경우가 많습니다. 물론 다른 곳에도 많이 쓰입니다만 자료를 찾아보면 눈에 쉽게 띄는 쪽은 텍스트 마이닝과 관련된 것 입니다. 텍스트에서 추출한 텀(term, 단어, 색인어)들의 빈도의 분포가 지수 스케일이기 때문에 벡터의 사잇각을 두고 비슷한 방향인지 아닌지를 보는 방법이고 이것이 비교적 합리적인 방법이기 때문입니다.
그리고 검색엔진에서 질의어로 본문을 찾아서 유사한 것을 찾는데 질의어와 본문이 가지고 있는 단어들의 빈도수 같은 것의 양적차이가 매우 크기 때문에 코사인 유사도가 유리합니다.
텍스트마이닝에서 코사인 유사도의 주의점
텍스트 데이터는 분량(데이터 사이즈)이 많기 때문에 코사인유사도 값을 구하려고 해도 현실에서는 컴퓨터 연산이 많이 소모되어서 하지 못하는 경우도 있습니다. 이런 작업을 하려면 사실은 대부분의 경우 분산 프로세싱을 수행해서 계산해야 합니다. 크기가 적당하다면 RDBMS를 사용하고 아니면 Hadoop이나 Spark같은 분산 컴퓨팅 환경(빅데이터 플랫폼)에서 작업해야 할 수도 있습니다.
Excel이나 R, Python으로는 계산하기에 너무 무거울 정도로 문서가 많고 그 상황에서도 코사인유사도 계산을 해야 한다면 코사인 유사도를 계산하는 과정을 완전히 이해 해두는 것이 나중에 코사인 유사도를 직접 구현해서 계산할 때를 위해서는 좋습니다.
요즘은 빅데이터 플랫폼들이 좋아서 기능을 기본 제공하는 경우도 많습니다. 그리고 어렵지 않게 구현할 수 있기 때문에 빅데이터 플랫폼으로 손쉽게 대량의 벡터들이나 텍스트데이터에서의 텀들의 유사도를 구할 수 있습니다.
텍스트 데이터를 가지고 코사인 유사도(Cosine Similarity)를 구해서 문서간의 유사도를 구하는 것은 다음 포스트에 해 보겠습니다.
코사인 유사도의 공식 유도?
코사인 유사도는 코사인 제2법칙에서 유도한 것이라고 되어 있고 실제로 유도가 됩니다. 여기서 유도하는 것은 설명하지 않겠습니다. 딱 한 번 해봤는데 기억도 안나고 하기 싫습니다. 재미 없습니다. 혹시 궁금하신 분은 자료를 찾아 보시면 그렇게 어렵지 않게 해볼 수 있습니다. 그런데 실제 응용에는 공식 유도가 크게 중요하지 않습니다.